Many graphics packages have functions to construct a 4-point-to-4-point transform of the type you need. For example, Qt has QTransform::quadToSquare and QTransform::quadToQuad, and OpenCV has GetPerspectiveTransform.
The transformation can not be linear or affine, it has to be a "perspective" transform.
If you want to code it yourself, this article tells you how. The formulae from that article are shown more clearly below:
If we want to transform the four points $(x_i, y_i)$ to the four points $(u_i, v_i)$ for $i=0,1,2,3$, we can use a perspective transform of the form:
$$
u_i = \frac{a_0 x_i + a_1 y_i + a_2}{c_0 x_i + c_1 y_i + 1 } \quad ; \quad
v_i = \frac{b_0 x_i + b_1 y_i + b_2}{c_0 x_i + c_1 y_i + 1 }
$$
The eight unknown coefficients $a_0, a_1, a_2, b_0, b_1, b_2, c_0, c_1$ can be calculated by solving the following linear system:
$$
\begin{bmatrix}
x_0 & y_0 & 1 & 0 & 0 & 0 & -x_0u_0 & -y_0u_0 \\
x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1u_1 & -y_1u_1 \\
x_2 & y_2 & 1 & 0 & 0 & 0 & -x_2u_2 & -y_2u_2 \\
x_3 & y_3 & 1 & 0 & 0 & 0 & -x_3u_3 & -y_3u_3 \\
0 & 0 & 0 & x_0 & y_0 & 1 & -x_0v_0 & -y_0v_0 \\
0 & 0 & 0 & x_1 & y_1 & 1 & -x_1v_1 & -y_1v_1 \\
0 & 0 & 0 & x_2 & y_2 & 1 & -x_2v_2 & -y_2v_2 \\
0 & 0 & 0 & x_3 & y_3 & 1 & -x_3v_3 & -y_3v_3
\end{bmatrix}
\begin{bmatrix}
a_0 \\
a_1 \\
a_2 \\
b_0 \\
b_1 \\
b_2 \\
c_0 \\
c_1
\end{bmatrix} =
\begin{bmatrix}
u_0 \\
u_1 \\
u_2 \\
u_3 \\
v_0 \\
v_1 \\
v_2 \\
v_3
\end{bmatrix}
$$
There are many available software packages for solving linear systems of equations.
One option is the "Numerical Recipes" book/package, which has functions called ludcmp and lubksb. The first of these computes the LU decomposition of a matrix, and then the second one uses this LU decomposition to solve a linear system. There is a long discussion of how to use ludcmp and lubksb here.
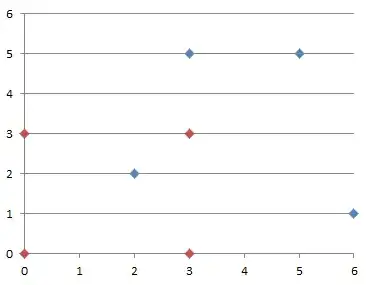
In your particular example, we have
$$
(x_0, y_0) = (3,5) \\
(x_1, y_1) = (5,5) \\
(x_2, y_2) = (2,2) \\
(x_3, y_3) = (6,1) \\
(u_0, v_0) = (0,3) \\
(u_1, v_1) = (3,3) \\
(u_2, v_2) = (0,0) \\
(u_3, v_3) = (3,0) \\
$$
The system of equations is
$$
3 a_0 + 5 a_1 + a_2 = 0 \\
5 a_0 + 5 a_1 + a_2 - 15 c_0 - 15 c_1 = 3 \\
2 a_0 + 2 a_1 + a_2 = 0 \\
6 a_0 + a_1 + a_2 - 18 c_0 - 3 c_1 = 3 \\
3 b_0 + 5 b_1 + b_2 - 9 c_0 - 15 c_1 = 3 \\
5 b_0 + 5 b_1 + b_2 - 15 c_0 - 15 c_1 = 3 \\
2 b_0 + 2 b_1 + b_2 = 0 \\
6 b_0 + b_1 + b_2 = 0
$$
I solved this system of equations using Mathematica, and I got
$$
a_0 = \frac{36}{49} \quad ; \quad
a_1 = -\frac{12}{49} \quad ; \quad
a_2 = -\frac{48}{49} \\
b_0 = \frac{24}{245} \quad ; \quad
b_1 = \frac{96}{245} \quad ; \quad
b_2 = -\frac{48}{49} \\
c_0 = \frac{8}{245} \quad ; \quad
c_1 = -\frac{33}{245}
$$
So, the required transformation (after some simplification) is
$$
u = \frac{60 (3 x-y-4)}{8 x-33 y+245} \\
v = \frac{24 (x+4 y-10)}{8 x-33 y+245}
$$
You can easily confirm that this transform maps the four given points correctly.