integrability of $f$ on $\Bbb R$ does not necessarily imply the convergence of $f(x)$ to $0$ as $x → ∞$

Question

I read that integrability of $f$ on $\Bbb R$ does not necessarily imply the convergence of $f(x)$ to $0$ as $x → ∞$. I am pretty sure that I also read somewhere something saying the opposite. Since I sometimes try to visualize graphically what is happening, then if $f$ does have a limit when $x \to \infty$, this limit must be zero, otherwise it would form a rectangle of infinite area and the integral would not be finite, more rigorously my claim is : if $\lim_\infty f(x)=L \in \Bbb R$ and $\int_\Bbb R f< \infty$, then $L=0$, and it can be proven the following way : if $L \neq 0$, then $\exists x_0$ such that $f(x) > \frac L2 \forall x > x_0$ and then $\int_\Bbb R f = \int_{- \infty} ^{x_0} f + \int_{x_0}^\infty f > \int_{- \infty} ^{x_0} f + \infty$ contradiction so $L=0$. Also, I sometimes think of improper integrals as series and in series, the infinite sum is finite if its sequence goes to $0$ which made me think the initial statement was weird. So that statement that says that integrability of $f$ on $\Bbb R$ does not necessarily imply the convergence of $f(x)$ to $0$ as $x → ∞$, is maybe based on a counterexample where $f$ does not have a limit. I was even told that there exists a positive continuous function $f : \Bbb R → [0, +∞)$ which is absolutely integrable and yet $f$ does not go to zero at infinity. To find such a function, I thought of some kind of function making a building at each odd integer but the width of the "stair" is quickly decreasing something like $2^{-k}$ for every odd integer $k$ (and $0$ for $x<0$). Is my function right ? If yes can it formulated more rigorously or is there an easier example I am not thinking of ?

I saw this Integrability of $f$ does not necessarily imply convergence of $f(x) \to 0$ as $x \to \infty$ but I strongly believe (I don't know why) that there exists some much easier example.

Answer 1

The question is interesting mainly if you ask it for continuous functions. Continuity, however, (as the other examples illustrate) is not sufficient, nor necessary.

Theorem 1. Suppose that $ f $ is continuous on $ [0,\infty) $ and that the improper integral $ \int_{0}^\infty f(x)\,dx $ converges. A necessary and sufficient condition on $ f $ so that $ f(x) \to 0 $ as $ x\to \infty $ is that $f$ is uniformly continuous.

This is textbook. It is rather more interesting (and not difficult) to prove that a continuous function that is not uniformly continuous cannot have that property. Then to exhibit an example, just pick your favorite integrable, but nonuniformly continuous function, as did @bjorn93. The picture in one of the answers for this problem shows the situation rather nicely.

Theorem 2. Suppose that $ f $ is Riemann integrable on every bounded interval contained in $ [0,\infty) $ and that the improper integral $ \int_{0}^\infty f(x)\,dx $ converges. A necessary and sufficient condition on $ f $ so that $ f(x) \to 0 $ as $ x\to\infty $ is given in this reference:

R. B. Kelman and T. J. Rivlin. Conditions for Integrand of an Improper Integral to be Bounded or Tend to Zero. The American Mathematical Monthly. Vol. 67, No. 10 (Dec., 1960), pp. 1019-1022.

I don't think it makes much sense to ask the question for the improper Lebesgue integral since that ignores a set of measure zero anyway.

P.S. This is the charitable answer. The other answer someone could (less charitably) offer is this. Take an arbitrary sequence of real numbers $\{c_n\}$ and define $f(n)=f(-n)=c_n$ for each integer $n$ and $f(x)=0$ otherwise. Then $\int_{-\infty}^{\infty} f(x)\,dx=0$. Want more? Take any integrable function $g$ and add $f$ to it. (Briefly, unless you specifically ask for continuous examples the problem is trivial.)

Answer 2

You have the right idea insofar as the broader question is concerned: if $\lim f(x) \ne 0$, you get a contradiction, but that in itself supposes the limit exists, so we have to seek some function where it doesn't if we want a counterexample.

The "tent" ideas there displayed algebraically, in the linked question, somewhat obfuscate what's going on. Consider the thought process for how such an example might be constructed, and why they are arguably one of the simplest examples to construct:

• "Okay, so I know to get a counterexample, I need to have the limit not exist. So I need some sort of oscillatory behavior."

• "For this to be a good and convincing counterexample, I should keep things simple. Triangular 'bumps' are easy to calculate the area of, and hence the integral over." (This is especially easy to rationalize since a number of counterexamples use similar ideas; exposure is nice.)

• "Clearly, a bunch of triangular waves of equal - or better, even growing - heights form a convincing argument for the nonexistence of the limit. Of course, the function should be zero outside of these triangles."

• "Of course, I want the area of the triangles, as I go to infinity, to converge. To make this convincing, I could construct the triangles to have areas in geometric progression: $1, 1/2, 1/4, 1/8$, and so on."

From there, you can fiddle around algebraically to find the algebraic description of a suitable function.

If you want the $n$th triangular bump to have area $1/2^n$, then you can let it have height $1$ and base length $1/2^{n-1}$. This would work for a constant height example; you can also have height $2^{n}$ and base $1/2^{2n-1}$, or some other such construct, for variable but increasing height.

Clearly the bases will be approaching zero length very fast, so you can choose points $x$ to serve as the "center" of the base, and make them, say, two or three units apart.

Then you can create an equation from the point at the desired height above each center, down to the base on either side, which describes your triangular bump, and define the rest of the function to be zero.

That would give you the algebraic description. In the end, it will look rather obtuse and people a little new to the subject will wonder "where in the hell did that come from" -- but it is, nonetheless, motivated geometrically with very basic ideas in mind.

I thought of some kind of function making a building at each odd integer but the width of the "stair" is quickly decreasing something like $2^{-k}$ for every odd integer $k$ (and $0$ for $x<0$). Is my function right ?

It can be made to work in a similar vein to the previous triangular spike idea, yes. The areas of these rectangles, assuming unit height, will approach $1$ or $2$ in the end, by use of the geometric series. (Which it is depends on whether $k=0$ is permissible, essentially.) However, the behavior ensures that the limit is nonzero (since there is always eventually another "jump up" to make the rectangle, eventually).

One way you could frame it algebraically is with the indicator function,

$$\mathbf{1}_A(x) = \begin{cases} 1 & x \in A \\ 0 & x \not \in A \end{cases}$$

Define a succession of sets $S_k$ (for $k \in \mathbb{Z}_{\ge 1}$) by the rule that

$$S_k = \left[ 2k+1 \;,\; 2k+1+\frac{1}{2^k} \right)$$

Then your function is

$$f(x) = \sum_{i=1}^\infty \mathbf{1}_{S_i}(x)$$

The details about $\int_\mathbb{R} f(x) \, \mathrm{d}x$ and $\lim f(x) \ne 0$ I leave for you to formulate to whatever degree of precision you desire.

So in the end, arguably, perhaps a simpler example after all, at least where the algebraic description is concerned. However, I do want the takeaway to not be that your answer is "significantly simpler", but rather - hopefully - you see how yours is motivated by similar ideas in the end as to the others in the linked question.

Namely: that in the question body:

Or Cookie's triangular spikes:

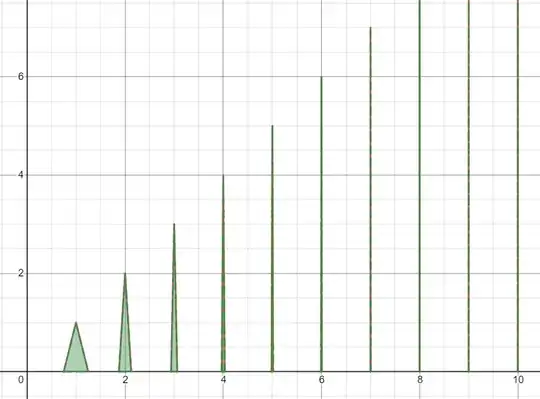
Or your own example:

Or, for the daring, bjorn93's suggestion of the Fresnel integral: