1

Integrability of $f$ on $\mathbb{R}$ does not necessarily imply the convergence of $f(x)$ to $0$ as $x \to \infty$.

(a) There exists a positive continuous function $f$ on $\mathbb{R}$ so that $f$ is integrable on $\mathbb{R}$, but yet $\operatorname{lim sup}_{x \to \infty} f(x)=\infty$

[Hint: For (a), construct a continuous version of the function equal to $n$ on the segment $[n,n+\frac 1{n^3})$, $n \ge 1$.]

Stein-Shakarchi: Chapter 2, Exercise 6(a)

Following the textbook's hint, I tried to define $$f(x)=\begin{cases}\frac {n^3}{x^2} & \text{if } x \in(-\infty,n) \\ n & \text{if }x \in [n,n+\frac 1{n^3}) \\ \frac{n(n+\frac 1{n^3})^2}{x^2} & \text{if } x \in (\frac 1{n^3},\infty),\end{cases}$$

so that $f$ is continuous, positive, and $\int_\mathbb{R} f(x) \, dx < \infty$. Will this make a good example? I do not know if $\operatorname{lim sup}_{x \to \infty} f(x)=\infty$.

Community
  • 1
Cookie
  • 13,532
  • It looks like you're using a single $n$, which won't work. You need to do something new for each integer $n$. – Rolf Hoyer Apr 12 '15 at 21:09
  • I would personally be happy with simply drawing a picture of an appropriate kind. If you make a tent at each $n \in \mathbb{N}$ so that the height of the tent goes to infinity with $n$, but such that the width goes to $0$ (in a sufficiently fast way to make the areas of the tents summable) you will get such a function. (This is the essence of the hint). – Frank Apr 12 '15 at 21:11
  • Hint about the hint: it will be good enough to approximate the discontinuous function by a a function whose graph comprises triangular spikes of height $n$ over the intervals $[n, n + \frac{1}{n^2}]$ and that is zero outside those intervals. – Rob Arthan Apr 12 '15 at 21:15
  • @RobArthan But zero is not positive, only non-negative. This problem calls for a positive $f(x)$. – Cookie Apr 12 '15 at 21:20
  • 1
    @dragon: good point. I misread your question. Adding any positive function that is integrable over $\mathbb{R}$ to the function that I described will do the job. – Rob Arthan Apr 12 '15 at 21:32
  • possible duplicate of Integrable function $f$ on $\mathbb R$ does not imply that limit $f(x)$ is zero –  Apr 19 '15 at 00:36
  • @pizza: The post you reference does not have the requirement that $f$ is positive, while this one does. Though the problems are very similar they do not seem to be duplicates. – Rory Daulton Apr 19 '15 at 05:13
  • @RoryDaulton Close enough for me. –  Apr 19 '15 at 05:15
  • @pizza That other question you pointed out is not the same; it lacks the positivity requirement that my question has, like Rory said, – Cookie Apr 19 '15 at 07:14
  • See this post https://math.stackexchange.com/questions/2527941/if-f-in-l1-bbb-r-dx-then-prove-that-for-almost-every-x-in-bbb-r-lim-lim

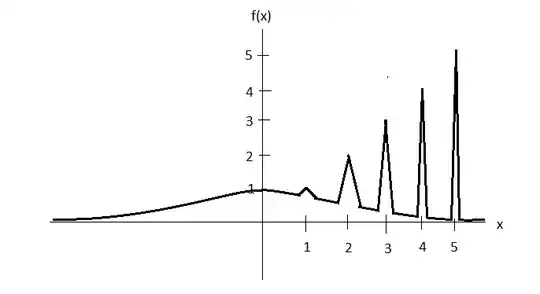
    Where the function is a Polynomial on each interval $[n, n+\frac{1}{2^n}]$ and zero elsewhere.

     – Guy Fsone Jun 10 '22 at 15:52

3 Answers3

2

Let $f(x)$ consist of either a function whose improper integral over $\mathbb{R}$ is finite or triangular spikes.

Each triangular spike is centered at $x=n$ and has base $\frac 1{2^n}$ and height $n$. Thus, the area of the triangular spikes are $$A_{\text{spikes}}=\sum_{n=1}^\infty \frac 12 \left(\frac 1{2^n}\right)(n)=1.$$

enter image description here

Therefore, $$\int_\mathbb{R} f(x) \, dx \le A_{\text{function}}+A_{\text{spikes}}<\infty.$$ And $f : \mathbb{R} \to \mathbb{R}$ is continuous, positive, and has $\text{lim sup}_{x \to \infty} f(x)=\infty$.

Community
  • 1
Cookie
  • 13,532
1

We take the "tent" idea and, to make it positive, we make "elsewhere" into a convergent (yet positive) integral, e.g. $\frac{1}{n^2}$.

So define $f$ piecewise as follows for each $n \geq 1$:

On $[n, n + \frac{1}{2n^3}]$ it is a straight line going from $\frac{1}{n^2}$ to $n$

On $[n + \frac{1}{2n^3}, n + \frac{1}{n^3}$ it is a straight line from $n$ to $\frac{1}{(n + \frac{1}{n^3})^2}$

On $[n + \frac{1}{n^3}, n+1]$ it is just $\frac{1}{x^2}$.

And then on $[0,1]$ we have $f = 1$ and $f = e^x$ on $(- \infty, 0]$.

The integral is then convergent.

MT_
  • 19,603
  • 9
  • 40
  • 81
-1

See the example in this post If $f\in L^1(\Bbb R,dx)$ then prove that for almost every $x\in\Bbb R$ $\lim\limits_{n\to \infty} f(nx) = 0.$

Where the function is a Polynomial on each interval $[n, n+\frac{1}{2^n}]$ and zero elsewhere.

Guy Fsone
  • 23,903