Evaluating $\int_{-\infty}^\infty \frac{\ln{(x^4+x^2+1)}}{x^4+1}dx$

Question

I recently attempted to evaluate the following integral $$\int_{-\infty}^\infty\frac{\ln{(x^4+x^2+1)}}{x^4+1}dx$$ I started by inserting a parameter, $t$ $$F(t)=\int_{-\infty}^\infty\frac{\ln{(tx^4+x^2+t)}}{x^4+1}dx$$ Where F(0) is the following $$F(0)=\int_{-\infty}^\infty\frac{\ln{(x^2)}}{x^4+1}dx=2\int_0^\infty\frac{\ln{(x^2)}}{x^4+1}dx=4\int_0^\infty\frac{\ln x}{x^4+1}dx$$ We can evaluate this using a common integral from complex analysis and taking the derivative using Leibniz’s rule. $$\int_0^\infty\frac{x^m}{x^n+1}dx=\frac{1}{m+1}\int_0^\infty\frac{(m+1)x^m}{(x^{m+1})^\frac{n}{m+1}+1}dx=\frac{1}{m+1}\int_0^\infty\frac{du}{x^\frac{n}{m+1}+1}$$ $$=\frac{1}{m+1}\frac{\pi}{\frac{n}{m+1}\sin{\frac{\pi}{\frac{n}{m+1}}}}=\frac{\pi}{n\sin{\frac{\pi(m+1)}{n}}}=\frac{\pi}{n}\csc{\frac{\pi(m+1)}{n}}$$ $$\int_0^\infty\frac{\ln{x}}{x^n+1}dx=\frac{d}{dm}\int_0^\infty\frac{x^m}{x^n+1}dx\Big|_{m=0}$$ $$=\frac{\pi}{n}\frac{d}{dm}\csc{\frac{\pi(m+1)}{n}}\Big|_{m=0}=-\frac{\pi^2}{n^2}\csc{\frac{\pi(m+1)}{n}}\cot{\frac{\pi(m+1)}{n}}\big|_{m=0}=-\frac{\pi^2}{n^2}\csc{\frac{\pi}{n}}\cot{\frac{\pi}{n}}$$ Therefore $$F(0)=4\int_0^\infty\frac{\ln{x}}{x^4+1}dx=-\frac{\pi^2\sqrt 2}{4}=-\frac{\pi^2}{2\sqrt 2}$$ Now that we found F(0), we can start applying Feynman’s trick. $$F’(t)=\int_{-\infty}^{\infty}\frac{dx}{tx^4+x^2+t}$$ Using a formula I derived we can continue $$\int_{-\infty}^\infty\frac{dx}{ax^4+bx^2+c}=\frac{\pi}{\sqrt{c}\sqrt{b+2\sqrt{ac}}}$$ $$F’(t)=\frac{\pi}{\sqrt{t}\sqrt{1+2t}}$$ Integrating both sides $$F(t)=\pi\sqrt2\ln{(\sqrt{2t}+\sqrt{2t+1})}+C$$ Set $t=0$ $$C=F(0)=-\frac{\pi^2}{2\sqrt2}$$ Therefore $$F(t)=\pi\sqrt2\ln{(\sqrt{2t}+\sqrt{2t+1})}-\frac{\pi^2}{2\sqrt2}$$ $$I=\pi\sqrt2\ln{(\sqrt2+\sqrt3)}-\frac{\pi^2}{2\sqrt2}$$ WolframAlpha confirms it numerically

I am not satisfied with this solution. I am curious as to what other solutions there might be. How else can we solve this integral?

Answer 1

Utilize the integral $\int_{-\infty}^\infty \frac{\ln(x^2+a^2)}{x^2+b^2}dx=\frac{2\pi}b \ln(a+b)$, along with the shorthands $p=e^{i\frac\pi6}$ and $q= e^{-i\frac\pi4} $ \begin{align} &\int_{-\infty}^\infty\frac{\ln{(x^4+x^2+1)}}{x^4+1}dx\\ =& \int_{-\infty}^\infty\frac{\ln{(x^2+p^2) (x^2+\bar{p}^2)}}{(x^2+q^2)( x^2+\bar{q}^2) }dx\\ =& \ \Im \int_{-\infty}^\infty \frac{\ln(x^2+p^2)}{x^2+{q}^2} + \frac{\ln(x^2+\bar{p}^2)}{x^2+{q}^2} \ dx\\ =& \ \Im \frac{2\pi}{q}\left[\ln (p+q)+\ln(\bar p+q)\right]\\ = &\ \sqrt2\pi\left( \ln(\sqrt2+\sqrt3)-\frac\pi4\right) \end{align}

Answer 2

\begin{align}J&=\int_{-\infty}^\infty \frac{\ln{(x^4+x^2+1)}}{x^4+1}dx\\ &=2\int_{0}^\infty \frac{\ln{(x^4+x^2+1)}}{x^4+1}dx\\ &=4\int_{0}^\infty \frac{\ln x}{1+x^4}dx+\underbrace{\int_{0}^\infty \frac{\left(1+\frac{1}{x^2}\right)\ln\left(\left(x-\frac{1}{x}\right)^2+3\right)}{\left(x-\frac{1}{x}\right)^2+2}dx}_{u=x-\frac{1}{x}}\\ &=4\int_{0}^\infty \frac{\ln x}{1+x^4}dx+\int_{-\infty}^\infty\frac{\ln(u^2+3)}{u^2+2}du\\ &=4\underbrace{\int_{0}^\infty \frac{\ln x}{1+x^4}dx}_{=A}+2\underbrace{\int_{0}^\infty\frac{\ln(u^2+3)}{u^2+2}du}_{B}\\ \end{align} Calculation of $B$.

Let \begin{align}a\in[0,1],F(a)&=\int_{0}^\infty\frac{\ln\Big(a(u^2+2)+1\Big)}{u^2+2}du,F(1)=B,F(0)=0\\ F^{\prime}(a)&=\int_0^\infty \frac{1}{1+a(2+x^2)}dx=\left[\frac{\arctan\left(\frac{ax}{\sqrt{a(1+2a)}}\right)}{\sqrt{a(1+2a)}}\right]_0^\infty=\frac{\pi}{2\sqrt{a(1+2a)}}\\ B&=\frac{\pi}{2\sqrt{2}}\left[\ln\left(1+4a+2\sqrt{2}\sqrt{a(1+2a)}\right)\right]_0^1=\boxed{\frac{\pi\ln\left(2\sqrt{6}+5\right)}{2\sqrt{2}}} \end{align}

Calculation of $A$.

\begin{align}R&=\int_0^\infty\int_0^\infty \frac{\ln(xy)}{(1+x^4)(1+y^4)}dxdy\\ &\overset{u(x)=xy}=\int_0^\infty \int_0^\infty \frac{y^3\ln u}{(1+y^4)(u^4+y^4)}dudy\\ &\frac{1}{4}\int_0^\infty\left[\frac{\ln\left(\frac{y^4+1}{y^4+u^4}\right)}{u^4-1}\right]_{y=0}^{y=\infty}\ln u du\\ &=\int_0^\infty \frac{\ln^2 u}{u^4-1}du\\ &=\frac{1}{2}\underbrace{\int_0^1 \frac{\ln^2 u}{u^2-1}du}_{=-\frac{\pi^3}{8}}-\frac{1}{2}\underbrace{\int_0^1 \frac{\ln^2 u}{1+u^2}du}_{=0}\\ &=\boxed{-\frac{\pi^3}{16}} \end{align}

On the other hand, \begin{align}R&=2A\int_0^\infty \frac{1}{1+u^4}du\\ \int_0^\infty \frac{1}{1+u^4}&=\int_0^\infty \frac{1+\frac{1}{u^2}}{\left(u-\frac{1}{u}\right)^2+2 }du\\ &\overset{z=u-\frac{1}{u}}= \int_{-\infty}^{+\infty}\frac{1}{2+z^2}dz=2\int_0^{+\infty}\frac{1}{2+z^2}dz\\ &=\left[\frac{\arctan\left(\frac{u}{\sqrt{2}}\right)}{\sqrt{2}}\right]_0^\infty=\boxed{\frac{\pi}{2\sqrt{2}}} \end{align}

Therefore,

\begin{align}A&=\frac{-\frac{\pi^3}{16}}{2\times \frac{\pi}{2\sqrt{2}}}=\boxed{-\frac{\pi^2}{8\sqrt{2}}}\\ J&=4A+2B=\boxed{-\frac{\pi^2}{2\sqrt{2}}+\frac{\pi\ln\left(2\sqrt{6}+5\right)}{\sqrt{2}}} \end{align}

NB: I assume,

\begin{align}\int_0^\infty \frac{\ln^2 x}{1+x^2}dx=\frac{\pi^3}{8}\end{align}

Answer 3

Solution using complex analysis

By substituting $x\mapsto\sqrt x$,

$$I = \int_{-\infty}^\infty \frac{\log(x^4+x^2+1)}{x^4+1} \, dx = \int_0^\infty \frac{\log(x^2+x+1)}{\sqrt x(x^2+1)} \, dx$$

Let $f(z)=\dfrac{\log\left(z^2+z+1\right)}{\sqrt z(z^2+1)}$ and integrate over a deformed circular contour $\mathcal C$ such that it avoids the branch points at $z\in\left\{0,e^{i\frac{2\pi}3},e^{i\frac{4\pi}3}\right\}$ and the respective cuts at $[0,\infty)$, $e^{i\frac{2\pi}3}[1,\infty)$, and $e^{i\frac{4\pi}3}[1,\infty)$. Label the "banks" along each $A$/$A'$, $B$/$B'$, and $C$/$C'$, where the unprimed banks are traversed away from the origin and vice versa.

---

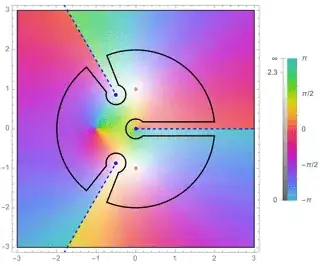
Parameterize the banks by

$$\begin{array}{c|cc|c|c} A & z = x + i\varepsilon & dz = dx & x\in[\varepsilon,R] & \arg(z)\to0 \\ A' & z = x - i\varepsilon & dz = dx & x\in[R,\varepsilon] & \arg(z)\to2\pi \\ \hline B & z = e^{i\left(\frac{2\pi}3+\theta\right)}x & dz = e^{i\left(\frac{2\pi}3+\theta\right)}\,dx & x\in[1+\varepsilon,R] & \arg\left(1+e^{i\frac\pi3}z\right)\to\pi \\ B' & z = e^{i\left(\frac{2\pi}3-\theta\right)}x & dz = e^{i\left(\frac{2\pi}3-\theta\right)}\,dx & x\in[R,1+\varepsilon] & \arg\left(1+e^{i\frac\pi3}z\right)\to-\pi \\ \hline C & z = e^{i\left(\frac{4\pi}3+\theta\right)}x & dz = e^{i\left(\frac{4\pi}3+\theta\right)}\,dx & x\in[1+\varepsilon,R] & \arg\left(1+e^{-i\frac\pi3}z\right)\to\pi\\ C' & z = e^{i\left(\frac{4\pi}3-\theta\right)}x & dz = e^{i\left(\frac{4\pi}3-\theta\right)}\,dx & x\in[R,1+\varepsilon] & \arg\left(1+e^{-i\frac\pi3}z\right)\to-\pi\\ \end{array}$$

where the last column shows the corresponding arguments to the relevant logarithm along the banks as we approach the cut from either side as $\varepsilon,\theta\to0$.

---

Expand the logarithm as

$$\log\left(z^2+z+1\right) = \log\left(z - e^{i\frac{2\pi}3}\right) + \log\left(z - e^{i\frac{4\pi}3}\right)$$

Compute the integrals along each path:

$$\begin{align*} \int_A f(z) \, dz = \int_\varepsilon^R f(x+i\varepsilon)\,dx &\to \int_0^\infty \frac{\log(x^2+x+1)}{\sqrt x(x^2+1)} \, dx \\[1ex] \int_{A'} f(z) \, dz = \int_R^\varepsilon f(x-i\varepsilon)\,dx &\to -\int_0^\infty \frac{\log(x^2+x+1)}{\sqrt x\,e^{i\pi} (x^2+1)} \, dx \\[1ex] \implies \int_{A\cup A'} f(z) \, dz &\to 2I \end{align*}$$

$$\begin{align*} \int_B f(z) \, dz = \int_{1+\varepsilon}^R f\left(e^{i\left(\frac{2\pi}3+\theta\right)}x\right)\,e^{i\left(\frac{2\pi}3+\theta\right)} \, dx &\to e^{i\frac{2\pi}3} \int_1^\infty \frac{\log(x-1)+i\pi+\log\left(e^{i\frac{2\pi}3}x - e^{i\frac{4\pi}3}\right)}{\sqrt x\,e^{i\frac\pi3}\left(e^{i\frac{4\pi}3}x^2+1\right)} \, dx \\[1ex] \int_{B'} f(z) \, dz = \int_R^{1+\varepsilon} f\left(e^{i\left(\frac{2\pi}3-\theta\right)}x\right)\,e^{i\left(\frac{2\pi}3-\theta\right)} \, dx &\to -e^{i\frac{2\pi}3} \int_1^\infty \frac{\log(x-1)-i\pi+\log\left(e^{i\frac{2\pi}3}x - e^{i\frac{4\pi}3}\right)}{\sqrt x\,e^{i\frac\pi3}\left(e^{i\frac{4\pi}3}x^2+1\right)} \, dx \\[1ex] \implies \int_{B\cup B'} f(z)\,dz &\to i2\pi \int_1^\infty \frac{e^{i\frac\pi3}}{\sqrt x\left(1-e^{i\frac\pi3}x^2\right)} \, dx \end{align*}$$

$$\begin{align*} \int_C f(z) \, dz = \int_{1+\varepsilon}^R f\left(e^{i\left(\frac{4\pi}3+\theta\right)}x\right)\,e^{i\left(\frac{4\pi}3+\theta\right)} \, dx &\to e^{i\frac{4\pi}3} \int_1^\infty \frac{\log\left(e^{i\frac{4\pi}3}x - e^{i\frac{2\pi}3}\right)+\log(x-1)+i\pi}{\sqrt x\,e^{i\frac{2\pi}3}\left(e^{i\frac{8\pi}3}x^2+1\right)} \, dx \\[1ex] \int_{C'} f(z) \, dz = \int_R^{1+\varepsilon} f\left(e^{i\left(\frac{4\pi}3-\theta\right)}x\right)\,e^{i\left(\frac{4\pi}3-\theta\right)} \, dx &\to -e^{i\frac{4\pi}3} \int_1^\infty \frac{\log\left(e^{i\frac{4\pi}3}x - e^{i\frac{2\pi}3}\right)+\log(x-1)-i\pi}{\sqrt x\,e^{i\frac{2\pi}3}\left(e^{i\frac{8\pi}3}x^2+1\right)} \, dx \\[1ex] \implies \int_{C\cup C'} f(z)\,dz &\to -i2\pi \int_1^\infty \frac{e^{-i\frac{\pi}3}}{\sqrt x\left(1-e^{-i\frac\pi3}x^2\right)} \, dx \end{align*}$$

---

The integrals over the arcs will vanish, and upon combining the bank integrals we have

$$\begin{align*} \oint_{\mathcal C} f(z) \, dz &= 2I - i2\pi \cdot i2\sqrt3 \int_1^\infty \frac{dx}{\sqrt x(1-x^2+x^4)} \\[1ex] &= 2I + 4\sqrt3\,\pi \int_1^\infty \frac{dx}{1-x^4+x^8} \end{align*}$$

Now get the residues at $z=\pm i$, whose sum will be $-i\frac{\pi}{2\sqrt2}$, so by Cauchy's residue theorem

$$\begin{align*} i2\pi \cdot \left(-i\frac{\pi}{2\sqrt2}\right) &= 2I + 4\sqrt3\,\pi \int_1^\infty \frac{dx}{1-x^4+x^8} \\[1ex] \implies I &= \frac{\pi^2}{2\sqrt2} - 4\sqrt3\,\pi \int_1^\infty \frac{dx}{1-x^4+x^8} \end{align*}$$

Plugging in the value of the remaining integral gives a result that agrees with the expected $I$. We can do it by partial fractions but with $8$ factors it's rather dull work.