2

I would like to understand statement of Cauchy integral theorem,which says that

Cauchy's integral theorem implies that the line integral of every holomorphic function along a loop vanishes: or

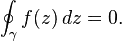
enter image description here

where γ is a rectifiable path in a simply connected open subset U of the complex plane C whose start point is equal to its end point, and $f : U → C$ is a holomorphic function. so first as i know rectifiable means finite,also because we have such complex plane whose start point is the same as end point,then does it means that it is similar to such situation when we have

$\int f(x)dx$ from $a$ to $b$ is equal to $F(b)-F(a)$ and because end and start point is same ,then this equals to zero? or there is two different path and they compensate each other?please help me to understand why this formula held?

Start wearing purple
  • 53,234
  • 13
  • 164
  • 223
dato datuashvili
  • 9,194

1 Answers1

1

One-line proof exploiting holomorphic of $f(z)$, Cauchy-Riemann equations and Stokes' theorem

Note that $f(z)\,dz$ is a closed differential form so:

$\int\limits_{\gamma}f(z)\,dz = \int\limits_{\partial D} f(z)\,dz = \int\limits_D d[f(z)\,dz] = 0 $

The $D$ is the area bounded by $\gamma$ countour.

igumnov
  • 809
  • could you be a little more detailed – dato datuashvili Jul 10 '13 at 14:46
  • Use some complex analysis book for detailed proofs of similar theorems. I studied this one few years ago http://math.stanford.edu/~ryzhik/shabat-all.pdf Chapter 2 – igumnov Jul 10 '13 at 15:12
  • This isn't quite true. The version of Cauchy integral theorem that the OP mentions is actually the Cauchy-Goursat integral theorem, whereas what your proof proves is the (classical) Cauchy integral theorem, in which $f'$ is assumed to be continuous (so that Green's/Stokes' theorem can be applied). Although some pointed out that the continuity of $f'$ can be made unnecessary, a special version of Stokes' theorem is needed. – user1551 Jul 11 '13 at 14:59
  • and generally what does this theorem says? – dato datuashvili Jul 12 '13 at 15:26
  • @dato See the Wikipedia article on the theorem. The theorem's statement is essentially the same as yours, but this actually is not the original Cauchy integral theorem. The original theorem, discovered by Cauchy himself, assumes that $f$ not only is holomorphic, but also has continuous partial derivatives on $U$. Goursat later found a new proof, in which the condition that $f'$ is continuous is removed. To distinguish between these two versions of the theorem, some called Goursat's version the Cauchy-Goursat theorem. – user1551 Jul 14 '13 at 12:57