Suppose we have a weak composition of the integer n into k parts. (A weak compositions is essentially a partition in which order matters and 0 is allowed)
My question is, what is the expected value of the largest part of the composition? The assumption is that all compositions have equal probability.
I'm going to give an exact answer in the form of a double sum and then a derivation showing why the approximation $$E[M] \approx \frac{H_k}{\log(1+k/n)} - \frac{1}{2}$$ using the maximum of geometric random variables (and mentioned by leonbloy) is an excellent one.
The Exact Expression. As Henry notes in the comments above, the expected largest part of the weak composition of $n$ into $k$ parts is 1 less than the expected largest part of (strong) compositions of $n+k$ into $k$ positive parts. Randomly decomposing $n+k$ into $k$ positive parts, in turn, is the same problem as taking a stick of length $n+k$ and breaking it at $k-1$ randomly chosen distinct integer points.
The last problem has been studied. If we let $M^+$ denote the largest piece, David and Nagaraja's Order Statistics, Problem 6.4.10, p. 155, gives, for $m \geq 1$, $$P(M^+ \leq m) = \frac{1}{\binom{n+k-1}{k-1}} \sum_{i=0}^k (-1)^i \binom{k}{i} \binom{n+k-1- mi}{k-1}.$$ (The approach is to consider the coefficient of $n+k$ in $(x + x^2 + \cdots x^m)^k$.) Thus $$E[M^+] = \sum_{m=0}^{n+k} \left(1 - \frac{1}{\binom{n+k-1}{k-1}} \sum_{i=0}^k (-1)^i \binom{k}{i} \binom{n+k-1- mi}{k-1}\right)$$ $$ = \sum_{m=0}^{n+k} \sum_{i=1}^k (-1)^{i+1} \binom{k}{i} \frac{\binom{n+k-1 -mi}{k-1}}{\binom{n+k-1}{k-1}}.$$ So the answer to the OP's question is just 1 less than this: $$E[M] = \sum_{m=1}^{n+k} \sum_{i=1}^k (-1)^{i+1} \binom{k}{i} \frac{\binom{n+k-1 -mi}{k-1}}{\binom{n+k-1}{k-1}} - 1,$$ which is exact but not as clean as we might like. (Note that this expression gives the same answers Henry obtained for small values of $n$ and $k$.)
The Approximation. While the double sum likely does not have a closed form, if we approximate the ratio of binomial coefficients using the known asymptotic for the ratio of gamma functions $\frac{\Gamma(z+a)}{\Gamma(z+b)} \approx z^{a-b}$ we get $$\frac{\binom{n+k-1-mi}{k-1}}{\binom{n+k-1}{k-1}} = \frac{(n+k-1-mi)! n!}{(n+k-1)! (n-mi)!} \approx (n+k)^{-mi} n^{mi} = \frac{1}{(1+k/n)^{mi}}.$$ So now we have $$E[M^+] \approx \sum_{i=1}^k (-1)^{i+1} \binom{k}{i} \sum_{m=0}^{n+k} \frac{1}{(1+k/n)^{mi}} \approx \sum_{i=1}^k (-1)^{i+1} \binom{k}{i} \sum_{m=0}^{\infty} \left(\frac{1}{(1+k/n)^i}\right)^m$$ $$ = \sum_{i=1}^k (-1)^{i+1} \binom{k}{i} \frac{1}{1 - (1+k/n)^{-i}}.$$
As I prove in my answer here, this is the expected maximum of a sample of size $k$ from a geometric distribution with parameter $p = 1 - q = 1- 1/(1+k/n)$. Then, in my answer here, I prove that this is very closely approximated by $\frac{1}{2} + \frac{1}{\lambda} H_k,$ where $\lambda = -\log (1-p)$. Therefore, we have, as mentioned by leonbloy, that $E[M]$ is very closely approximated by $$E[M] \approx \frac{H_k}{\log(1+k/n)} - \frac{1}{2}.$$
I can't provide an explicit answer, but this might help investigations:
Using the following R code
library(gtools)
library(matrixStats)
mean_max_weak_compositions <- function(total,parts) {
co <- cbind(rep(0, choose(total+parts-1, parts-1)),
combinations(total+parts-1, parts-1) ,
rep(total+parts, choose(total+parts-1, parts-1)) )
mean(rowMaxs(co[,-1] - co[,-(parts+1)])) - 1 }
vmmwc <- Vectorize(mean_max_weak_compositions)
means <- cbind(1:15, outer(1:15, 2:10, FUN="vmmwc"))
produces the following table of expected maximum values, where the number of parts goes horizontally and the total goes vertically
> means
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
[2,] 2 1.666667 1.500000 1.400000 1.333333 1.285714 1.250000 1.222222 1.200000 1.181818
[3,] 3 2.500000 2.200000 2.000000 1.857143 1.750000 1.666667 1.600000 1.545455 1.500000
[4,] 4 3.200000 2.800000 2.542857 2.357143 2.214286 2.100000 2.006061 1.927273 1.860140
[5,] 5 4.000000 3.428571 3.071429 2.825397 2.642857 2.500000 2.383838 2.286713 2.203796
[6,] 6 4.714286 4.035714 3.595238 3.285714 3.056277 2.878788 2.736597 2.619381 2.520480
[7,] 7 5.500000 4.666667 4.133333 3.757576 3.477273 3.259907 3.086247 2.944056 2.825175
[8,] 8 6.222222 5.266667 4.654545 4.222222 3.897436 3.643357 3.438850 3.270629 3.129782
[9,] 9 7.000000 5.890909 5.181818 4.685315 4.314685 4.025175 3.791608 3.598684 3.436446
[10,] 10 7.727273 6.500000 5.706294 5.146853 4.729271 4.403846 4.141711 3.925134 3.742666
[11,] 11 8.500000 7.115385 6.230769 5.608059 5.142857 4.780543 4.489191 4.248869 4.046559
[12,] 12 9.230769 7.725275 6.753846 6.068681 5.556076 5.156486 4.835239 4.570564 4.348076
[13,] 13 10.000000 8.342857 7.278571 6.529412 5.969188 5.532250 5.180805 4.891287 4.648104
[14,] 14 10.733333 8.950000 7.800000 6.988562 6.381321 5.907430 5.525972 5.211540 4.947393
[15,] 15 11.500000 9.566176 8.323529 7.447884 6.792957 6.281992 5.870626 5.531382 5.246255
Plotting this (totals on the horizontal axis, expectations of maximum values on the vertical axis, and numbers of parts as coloured digits) looks like
The expectations of maximum values seem to grow close to linearly to the totals, but to fall more slowly than inversely to the number of parts.
Added
For small $n$ it is possible to the express the expected value of the largest part of the composition explictly as a polynomial ratio, such as:
$$E_{\max}(1,k) = 1$$
$$E_{\max}(2,k) = 1+\frac{2}{k+1}$$
$$E_{\max}(3,k) = 1+\frac{6(k+1)}{(k+1)(k+2)}$$
$$E_{\max}(4,k) = 1+\frac{12(k^2+2k+3)}{(k+1)(k+2)(k+3)}$$
$$E_{\max}(5,k) = 1+\frac{20(k^3+3k^2+14k+6)}{(k+1)(k+2)(k+3)(k+4)}$$
$$E_{\max}(6,k) = 1+\frac{30(k^4+4k^3+39k^2+32k+44)}{(k+1)(k+2)(k+3)(k+4)(k+5)}$$
and there are enough obvious patterns in the coefficients of the numerators to be able to suggest a reasonable approximation for cases of $k$ very much greater than $n$.
Here's my asymptotic approach:
Let consider the (equivalent, as pointed out by Henry) case of strong compositions of $n+k=m$ into $k$ positive parts.
In probabilistic terms, we have $k$ random variables $x_i$ taking values on $1\cdots m$, with $\sum x_i =m$ and were all the possible realizations are equiprobable.
I claim (if my life does not depend on it) that that problem is asymptotically equivalent (why? in what sense? explained below) to having $k$ iid geometric random variables $y_i$ (taking values on $1\cdots \infty$) with mean $m/k=1/p$ (notice that here $\sum y_i$ is not fixed, but $E[\sum y_i] =m$).
Then, a first approximation would be
$\displaystyle E_M = E(max(x_i)) -1 \approx E(max(y_i)) -1 = G\left(k,\frac{k}{k+n}\right) - 1$
where $G(k,p)$ is the expectation of the maximum of $k$ IID geometric random variables of parameter $p$. This later problem is discussed here and here. The exact formula is rather complicated:
$\displaystyle G(k,p) = \sum_{i=1}^k \binom{k}{i} (-1)^{i+1} \frac{1}{1-(1-p)^i}$
A tight approximation is given by:
$\displaystyle G(k,p) \approx \frac{H_k}{- \log(1-p)} + \frac{1}{2} $ , with $\displaystyle H_k=\sum_{i=1}^k \frac{1}{i}$ (harmonic number).
what gives our second approximation:
$\displaystyle E_M \approx \frac{H_k}{\log(1+k/n)} - \frac{1}{2}$
And for $n$ increasing with $k$ constant, the first order expansion of the logarithm gives this third approximation, which shows the linear increasing observed by Henry:
$\displaystyle E_M \approx n \frac{ H_k} {k} - \frac{1}{2} \approx n \frac{ H_k} {k}$ $ \hspace{14pt} (n \to \infty)$
It is also readily seen that if both $n,k$ increase with constant ratio, then $E_M$ grows as $\log(k)$.
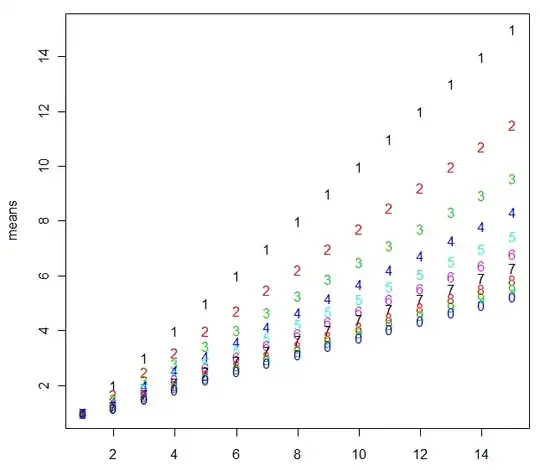
Some results, for comparing with Henry's values, for the second approximation (very similar to the first one; the third one is quite more coarse)
1 2 3 4 5 6 7 8 9 10
1 0.9427 0.8654 0.8225 0.7944 0.7744 0.7591 0.7469 0.7370 0.7286 0.7215
2 1.9663 1.6640 1.5008 1.3963 1.3226 1.2673 1.2239 1.1887 1.1595 1.1347
3 2.9761 2.4364 2.1449 1.9588 1.8280 1.7301 1.6536 1.5918 1.5407 1.4975
4 3.9814 3.1995 2.7761 2.5056 2.3157 2.1738 2.0631 1.9739 1.9002 1.8380
5 4.9848 3.9580 3.4007 3.0444 2.7942 2.6073 2.4617 2.3444 2.2476 2.1661
6 5.9872 4.7141 4.0216 3.5784 3.2670 3.0346 2.8535 2.7077 2.5874 2.4862
7 6.9889 5.4686 4.6401 4.1093 3.7363 3.4577 3.2407 3.0661 2.9221 2.8010
8 7.9902 6.2221 5.2570 4.6381 4.2030 3.8780 3.6248 3.4210 3.2531 3.1119
9 8.9912 6.9749 5.8728 5.1655 4.6679 4.2962 4.0065 3.7734 3.5813 3.4198
10 9.9921 7.7272 6.4877 5.6917 5.1314 4.7127 4.3864 4.1239 3.9075 3.7256
11 10.9927 8.4791 7.1021 6.2171 5.5939 5.1281 4.7649 4.4728 4.2320 4.0296
12 11.9933 9.2307 7.7159 6.7418 6.0555 5.5424 5.1424 4.8205 4.5552 4.3322
13 12.9938 9.9821 8.3294 7.2660 6.5165 5.9560 5.5189 5.1672 4.8773 4.6336
14 13.9943 10.7333 8.9426 7.7897 6.9770 6.3690 5.8948 5.5132 5.1985 4.9341
15 14.9946 11.4844 9.5555 8.3132 7.4370 6.7814 6.2700 5.8584 5.5190 5.2338
Some (loose) justification about the aproximation. For those who are familiar with statistical physics, this is much related with a hard-rod (unidimensional) gas, over a discrete space, with the distance between consecutive particules as variables, and the (asympotical) equivalence of two "ensembles": the original has fixed volume (m) and number of particles (k) (that would correspond to a "canonical" ensemble), the second keeps the number of particles but the volume is allowed to vary (would be an isobaric ensemble), but such that the mean volume is equal to the fixed volume of the original. The condition that the configurations of the original ensemble have equal probability is related to a system with no interaction energy (except for the exlusion), and that corresponds (in the second ensemble) to a particle that can appear at each cell with a probability independent of its neighbours: and from here I got the geometrical.
In other terms, the equivalence might be justified in that the second probalistic model is equal to the first if conditioned on the event that the variables sum up to $m$ - and asymptotically we are less likely to depart from this case.
All this does not provide a rigorous proof, of course. One could also object that this kind of approximation by "ensemble equivalence" is plausible for computing the typical statistical magnitudes that are mostly related to averages - but here we are computing extreme value, it's less clear that it must work.
Added: Some clarification about the aproximation method:
Recall that ${\bf x}=\{x_i\}$ , $i=1\cdots k$ is our original discrete random variable; it support is restricted by $x_i\ge 1$ and $\sum x_i = m= n+k$. Inside this region, all realizations has equal probability, so the probability function is constant:
$P({\bf x}) = \frac{1}{Z}$
( $Z(n,k)$, the "partition function", would be the count of all possible configurations, but that does not matter here).
On the other side, the proposed ${\bf y}=\{y_i\}$ has iid geometric components, with parameter $p=k/m$, so its probability function is
$\displaystyle P({\bf y}) = \prod p (1-p)^{y_i} = p^k (1-p)^{\sum y_i}$
with $y_i \ge 1$. Calling $ s({\bf y})=\sum y_i$, it is readily seen that if we condition on $s = m$, we get the original distribution (it's constant, and in the same region).
$P({\bf y} | s = m ) = P({\bf x})$
We are interested in $E[g({ \bf x})]$, where $g({\bf x}) = max(x_1 \cdots x_k)$, and want to see if it can be approximated by $E[g({\bf y})]$ (some loose notation here)
$\displaystyle E[g({\bf y})] = \int g({\bf y}) P({\bf y}) dy = \int g({\bf y}) \sum_s P({\bf y} | s) P(s) dy $
Now, because the way we choose $p$, we have $E(s)=m$, and we can expect that $P(s)$ will be highly peaked around that value (to show that the statistical ensembles -canonnical, microcanonical, grand-canonical, etc- are asympotically equivalent, one uses this line of reasoning ). And so, asympotically, we can expect to be justified in aproximate the sum by that single term. What would mean that
$E[g({\bf y})] \approx E[g({\bf x})]$
