$k$ balls are uniformly and independently placed into $n$ bins. Sort the bins in ascending order. Is there a general formula for the expected number of balls in the $i$th ordered bin?
I don't really have an idea for how to approach this. I only got as far as figuring out that the probability of an arbitrary bin containing $m$ balls is $(1/n)^m (1-1/n)^{k-m} {k \choose m}$. I worked out the case for $n=2$, but that's so trivial I doubt it would help with a general solution.
The graph of the formula in question looks pretty interesting. X-axis is $i$, Y-axis is expected value of $i$th bin, for $k=100$ and $n=100$. I generated it by averaging 10,000 random placements.
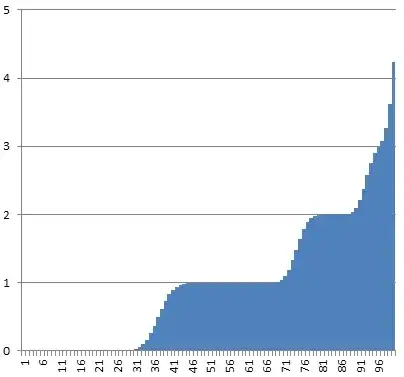
{{0,0,4}, {0,1,3}, {0,2,2}, {0,3,1}, {0,4,0}, {1,0,3}, {1,1,2}, {1,2,1}, {1,3,0}, {2,0,2}, {2,1,1}, {2,2,0}, {3,0,1}, {3,1,0}, {4,0,0}}... and you attach equal probability to each sequence occurring ... Is that a correct description of your set-up? – wolfies Dec 20 '13 at 18:50