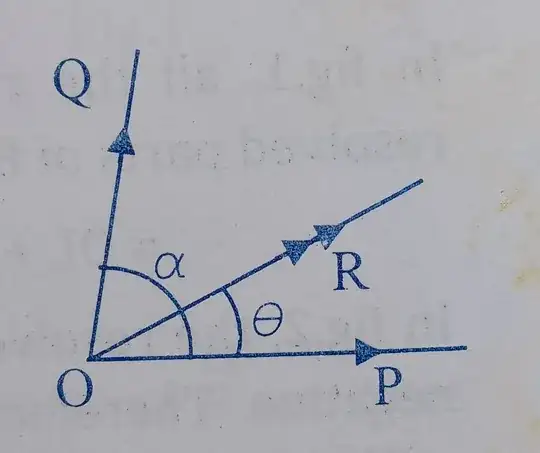0

Question:

Two forces $\vec{P}$ and $\vec{Q}$ acting at a point have a resultant $\vec{R}$ and the resolved part of $\vec{R}$ along $\vec{P}$ is equal to the magnitude of $\vec{Q}$. Prove that the angle between the forces is $\alpha=2\sin^{-1}\left(\sqrt{\frac{P}{2Q}}\right)$.

My book's attempt:

enter image description here

$$P+Q\cos\alpha=Q$$

$$P=Q(1-\cos\alpha)$$

$$\frac{P}{Q}=2\sin^2\frac{\alpha}{2}$$

$$\frac{P}{2Q}=\sin^2\frac{\alpha}{2}$$

$$\sqrt{\frac{P}{2Q}}=\sqrt{\sin^2\frac{\alpha}{2}}\tag{1}$$

$$\sqrt{\frac{P}{2Q}}=\sin\frac{\alpha}{2}\tag{2}$$

$$\sin\frac{\alpha}{2}=\sqrt{\frac{P}{2Q}}$$

$$\sin^{-1}(\sin\frac{\alpha}{2})=\sin^{-1}\left(\sqrt{\frac{P}{2Q}}\right)\tag{3}$$

$$\frac{\alpha}{2}=\sin^{-1}\left(\sqrt{\frac{P}{2Q}}\right)\tag{4}$$

$$\alpha=2\sin^{-1}\left(\sqrt{\frac{P}{2Q}}\right)$$

My comments:

They managed to prove what was given in the question, but their procedure is questionable in my opinion. Up to $(1)$, everything is correct, but in $(2)$, they did this $\sqrt{\sin^{2}\frac{\alpha}{2}}=\sin\frac{\alpha}{2}$. Shouldn't it have been $\sqrt{\sin^{2}\frac{\alpha}{2}}=|\sin\frac{\alpha}{2}|$? Also didn't they discard a lot of legitimate solutions in $(4)$ (related)?

My questions:

  1. Are lines $(2)$ and $(4)$ valid?
tryingtobeastoic
  • 3,176

1 Answers1

2

Line 2: Since $\alpha/2 \leq \pi$, $\sin(\alpha) \geq 0$, so $|\sin(\alpha)| = \sin(\alpha)$

Line 4: $\sin^{-1}(\sin(x)) = x$ when $-\pi/2 \leq x \leq \pi/2$. Since $\alpha/2$ is between that range (the angle between two vectors cannot be greater than $\pi$), this is legitimate.

David Lui
  • 6,295
  • If the angle between two vectors is $\alpha$ and $π>\alpha>\frac{π}{2}$, then isn't $(4)$ incorrect as $\alpha$ lies outside the range of arcsin function? – tryingtobeastoic Feb 25 '22 at 06:17
  • 1
    $\alpha$ is between $0$ and $\pi$ ,so $\alpha/2$ is between $0$ and $\pi/2$, so $\sin^{-1}(\sin(x)) = x$. – David Lui Feb 25 '22 at 07:30