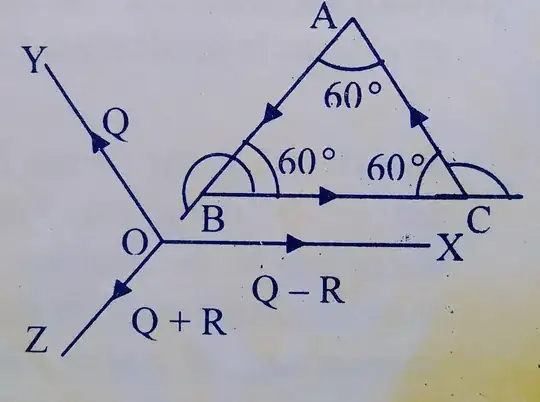
Question:
Forces of magnitude $Q-R$, $Q$, $Q+R$ act at a point in directions parallel to the sides of an equilateral triangle taken in order. Find the magnitude of their resultant.
My attempt:
Let
$$F_1=Q\cos(120^{\circ})+(Q+R)\cos(120^{\circ})+(Q-R)\cos(0^{\circ})$$
$$...$$
$$F_1=-\frac{3}{2}R$$
Again, let
$$F_2=Q\sin(120^{\circ})+(Q+R)\sin(120^{\circ})+(Q-R)\sin(0^{\circ})$$
$$...$$
$$F_2=\frac{2\sqrt{3}Q+\sqrt{3}R}{2}$$
Now,
$$F=\sqrt{F_1^2+F_2^2}$$
$$...$$
$$F=\frac{1}{2}\sqrt{12(Q^2+QR+R^2)}\tag{Ans.}$$
My book's attempt:
Let
$$F_1=Q\cos(180^{\circ}-60^{\circ})+(Q+R)\cos(180^{\circ}+60^{\circ})+(Q-R)\cos(0^{\circ})\tag{#}$$
$$...$$
$$F_1=-\frac{3}{2}R$$
Again, let
$$F_2=Q\sin(180^{\circ}-60^{\circ})+(Q+R)\sin(180^{\circ}+60^{\circ})+(Q-R)\sin(0^{\circ})\tag{*}$$
$$...$$
$$F_2=-\frac{\sqrt{3}}{2}R$$
Now,
$$F=\sqrt{F_1^2+F_2^2}$$
$$...$$
$$F=\sqrt{3}R\tag{Ans.}$$
My comments:
My answer is different than that of my book's. Also, my $F_2$ is different than that of my book's $F_2$. Also, how come my book wrote $(Q+R)\cos(180^{\circ}+60^{\circ})$ and $(Q+R)\sin(180^{\circ}+60^{\circ})$ in $(\#)$ and $(*)$ respectively? Isn't it true that the angle between two vectors can't be greater than $180^{\circ}$?
Question:
- Why did I get a different answer than that of my book's?