Show that $$1^3+2^3+3^3+\text{...}+n^3=(1+2+3+\text{...}+n)^2$$ For $n=1$ we have $$1^3=1^2$$ which is obviously true. Assume that $$1^3+2^3+3^3+\text{...}+k^3=(1+2+3+\text{...}+k)^2$$is true for some positive integer $k\ge1$. We shall now prove that it is also true for $n=k+1$. I don't see how can we do that. $$1^3+2^3+3^3+\text{...}+k^3+(k+1)^3\overset{?}{=}(1+2+3+\text{...}+k+(k+1))^2$$ The LHS is $$(1+2+3+\text{...}+k)^2+(k+1)^3=...$$
Asked
Active
Viewed 139 times
-1
-
Hint: it's a lot easier if you can assume (or show by induction) that $1 + 2 + \dots + k = \frac 12 k(k+1)$ first. – Deepak Jan 16 '22 at 11:39
-
A more interesting question, IMHO is: find a geometric proof of this statement. – Igor Rivin Jan 16 '22 at 11:43
-
See for example https://math.stackexchange.com/q/1125766/42969 or https://math.stackexchange.com/q/1111443/42969 or https://math.stackexchange.com/q/996083/42969 – Martin R Jan 16 '22 at 11:45
-
1For a visual proof, see https://math.stackexchange.com/q/3938027/42969. – Martin R Jan 16 '22 at 11:46
-
1For what it's worth, I posted an answer and then deleted it, because my answer is a duplicate. – user2661923 Jan 16 '22 at 11:57
-
@EliasCosta, obviously I wasn't familiar with the fact that $1+2+\text{...}+k=\dfrac12k(k+1)$, so no. – kormoran Jan 16 '22 at 12:02
2 Answers
1
You need to show that $1^3 + 2^3 + \dots + k^3 + (k+1)^3 = (1+2+ \dots + k+k+1)^2$.
It's a lot easier if you can assume (or show by induction) that $1 + 2 + \dots + k = \frac 12 k(k+1)$ first.
Using that result,
$1^3 + 2^3 + \dots + k^3 + (k+1)^3 \\= (\frac 12k(k+1))^2 + (k+1)^3 \\= (\frac12)^2(k+1)^2(k^2 + 4k +4) \\= (\frac12)^2(k+1)^2(k+2)^2 \\= (1 + 2 + \dots + k+k+1)^2$
as required.
Deepak
- 26,801
-
Thank you for the response! Can you clarify how $$(\frac12)^2(k+1)^2(k+2)^2)$$ is equal to the RHS? – kormoran Jan 16 '22 at 12:01
-
See the duplicate for an induction proof. This question has been asked several times already. – Dietrich Burde Jan 16 '22 at 12:03
-
1@Medi That's equal to $(\frac 12(k+1)(k+2))^2 = (1 + 2 + \dots + k+1)^2$. It's basically reversing the lemma I asked you to show first. Do you see? – Deepak Jan 16 '22 at 12:10
-
@DietrichBurde Sorry, I get your point, and what you wrote is true. I did want to help the OP out as they wrote a good quality question and gave good details of their doubt. – Deepak Jan 16 '22 at 12:11
-
-
@DietrichBurde, if you can't help me, I really don't see what's the point of you writing useless comments under people's tries to assist me. – kormoran Jan 16 '22 at 12:15
0
Here's a beautiful visual proof. I got the picture from Google.
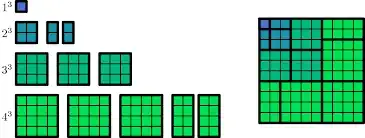
The blocks on the left are of course cubes and not squares as they may look like.
Sayan Dutta
- 8,831
-
-
@DietrichBurde no, I didn't see that. That one's nicer of course. But, that's no reason for the downvote- my answer is correct and I put my own effort in it. – Sayan Dutta Jan 16 '22 at 17:41