3

I was studying the Bisection method for root finding. It states that for a continuous function we can find out a root if it exists by the Intermediate value theorem.My question is why do we need Continuity of a function? Can't I just work with a function having just the intermediate value property without being continuous?

Upstart
  • 2,613

1 Answers1

3

For the sake of completeness, we mention that a function is Darboux on an interval $I$ if it has the intermediate value property. That is, for any $a,b\in I$ with $a<b$ and for any $y$ between $f(a)$ and $f(b)$, there is a $c$ between $a$ and $b$ such that $y=f(c)$.

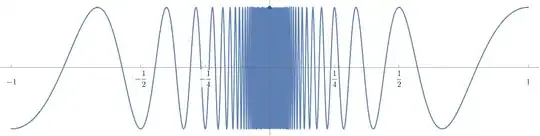
Continuous function are Darboux by the intermediate value theorem but there are discontinuous functions that are Darboux as well. One example is $$ f(x) = \begin{cases} \cos\left(\frac{2\pi}{x}\right) & x > 0 \\ -\cos\left(\frac{2\pi}{x}\right) & x < 0 \\ 1 & x = 0. \end{cases} $$ whose graph looks like so:

enter image description here

I think it's pretty easy to see that $f$ is Darboux. Also note that $$f\left(\pm \frac{1}{k}\right) = \pm 1$$ for all $k\in\mathbb N$.

Now, ff we apply the bisection method over the interval $[-1,1]$, we generate the following sequence of nested intervals: $$ \begin{aligned} I_0 & = [-1,1], \\ I_1 & = [-1,0], \\ I_2 & = \left[-\frac{1}{2},0\right], \: \: (\text{since } f(0) = 1) \\ \vdots & = \: \: \: \: \vdots \\ I_n & = \left[\frac{1}{2^{n-1}},0\right]. \end{aligned} $$

We can now see the problem pretty clearly. The bisection method will generate a nested sequence of intervals collapsing down to a point (zero in, this case) but, without continuity, that point need not be a root of the function.

Mark McClure
  • 30,510
  • Is this specific if we took the interval $[-1,1]$ or no interval would ever work. Because even I took an interval $[-1,5]$ but still could not get the root $x=4$. – Upstart Jan 13 '22 at 12:05
  • I think that most intervals would lead to a sequence that converges to some root. If $I_0 = [3,5]$, then you'll get zoom into $x=4$. More generally, once both endpoints of $I_n$ have the same sign for some $n$, convergence to a root is guaranteed. I had to choose the function and interval fairly carefully to avoid convergence to a root. – Mark McClure Jan 13 '22 at 13:25
  • Once both endpoints of.......convergence to a root is guaranteed. Why do you say this? – Upstart Jan 13 '22 at 14:58
  • @Upstart Convergence (for this specific example) is guaranteed for an interval on either side of the origin because the function is continuous away from the origin so the intermediate value theorem applies. – Mark McClure Jan 13 '22 at 15:52
  • Okay I got it. If I may ask how did you construct this function. I am getting a feel that this function might have been a part of a derivative of some function. Since derivatives have Datboux property – Upstart Jan 13 '22 at 16:43
  • Functions like $\cos(1/x)$ are part of any analyst's repertoire. While they can arise as derivatives of other important functions (as I explain in this answer), that was not my starting point. I simply started with $\cos(1/x)$ and scaled it in such a way that its value would be 1 when $x=1/2^n$ but $-1$ when $x=-1/2^n$. The rest kind of followed. – Mark McClure Jan 13 '22 at 16:52
  • Okay glad that you could elaborate. – Upstart Jan 13 '22 at 16:54