EDIT: I realize now, after writing it, that I did not answer the asker's original question at all. Feel free to downvote me, but I sorta put a bit too much time into this answer so I think I'll leave it here if people want to read it, but understand that it doesn't answer the asker's original question. Again, feel free to downvote.
The "moving particle" explanation was the final explanation that gave me an intuitive grasp on the subject. It is elaborated in the book Visual Complex Analysis by Tristan Needham, and I recommend looking at it if you ever get the chance.
The basic principle is this: Say that the position of a particle in the complex plane is given by $\mathbf{r} = e^{i \omega t}$, parameterized by $\mathbf{r} = < x(t),\ y(t) >$. If we can find $x(t)$ and $y(t)$, we will be able to find the real and imaginary parts of $e^{it}$.
Let's consider the velocity of this particle, $\mathbf{v} = \dot{\mathbf{r}}$, or $\frac{d\mathbf{r}}{dt}$. This is pretty simple; $i$ is simply a constant number, so $\dot{\mathbf{r}} = i \omega e^{i \omega t}$.
As you know, multiplication by $i$ is the same as a rotation by $\pi/2$ counter-clockwise in the complex plane.
Basically, this tells us that the velocity of our particle is perpendicular to its position vector.
If we find the acceleration of the particle, we get $\ddot{\mathbf{r}} = - \omega^2 e^{i \omega t}$. As you know, multiplcation by $-1$ is the same as a rotation by $\pi$ in the complex plane.
We can rewrite the acceleration as $\ddot{\mathbf{r}} = - \omega^2 \mathbf{r}$. Conceptually, this is saying that the acceleration of our particle is always in the opposite direction of the position vector (that is, towards the origin) with a magnitude proportional to the square of the angular velocity.
What kind of motion do we know behaves this way?
That's right -- motion in a circle around the origin.
This behaves exactly like $\mathbf{r} = < cos(\omega x),\ sin(\omega t) >$. Its velocity is $\dot{\mathbf{r}} = \omega < -sin(\omega x),\ cos(\omega t) >$, which is $\mathbf{r}$ rotated $\pi/2$ radians counter-clockwise. Its acceleration is $\ddot{\mathbf{r}} = -\omega^2 < cos(\omega x),\ sin(\omega t) > = - \omega^2 \mathbf{r}$.
You will find that the solution $\mathbf{r} = < cos(\omega x),\ sin(\omega t) >$ one of the solutions for the system of differential equations $\dot{\mathbf{r}} = i \omega \mathbf{r}$ and $\ddot{\mathbf{r}} = - \omega^2 \mathbf{r}$.
If we throw in our initial condition that $\mathbf{r}(0) = 1$ (that is, $e^{0 i \omega} = 1$), we find that $\mathbf{r} = < cos(\omega x),\ sin(\omega t) >$ is our unique solution to the differential equations. (Please correct me if I'm wrong --- I'm trying to think of other cases. I'm thinking there should be another constraint, but I can't think of it.).
So, $\mathbf{r} = < cos(\omega x),\ sin(\omega t) >$.
Therefore, $e^{i \omega t} = cos(\omega t) + i sin(\omega t)$
$e^{i \theta} = cos(\theta) + i sin(\theta)$
Where $e^{i \theta}$ parameterizes a particle that has moved through a circle an angular distance $\theta = \omega t$
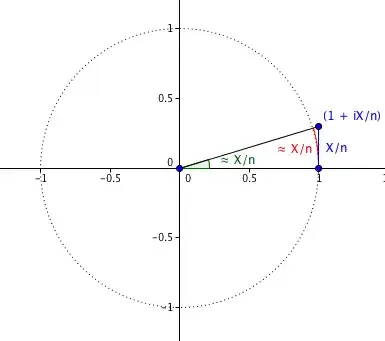
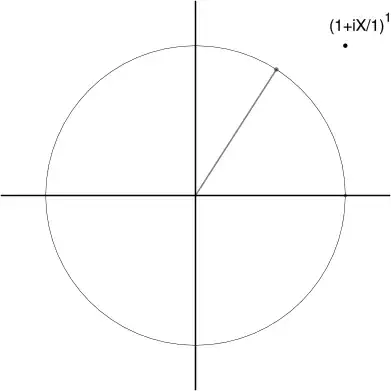
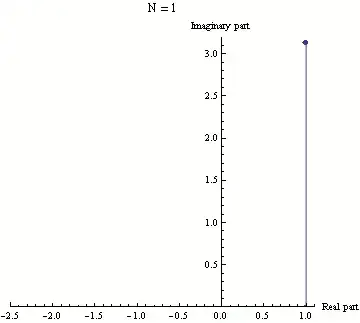
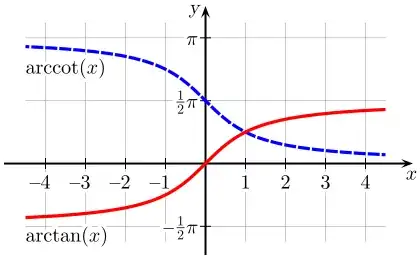 We can see that for really small values of x, $\arctan(x)$ is about x. So $\arctan {\frac{\theta}{n}} $ is about $\theta / n$. This is more accurate as n gets larger.
We can see that for really small values of x, $\arctan(x)$ is about x. So $\arctan {\frac{\theta}{n}} $ is about $\theta / n$. This is more accurate as n gets larger.