Where do the circles go when you stereographically project the dodecahedron?

Question

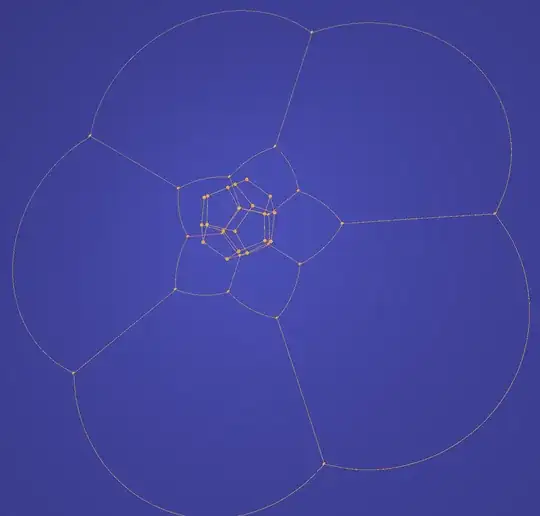
I'm going to ask what I think is surely a silly and simple question but I can't for the life of me work this out. I am interested in stereographically projecting a dodecahedron to the plane (in an interactive computer program). This has been implemented and here is an example image:

Now, imagine that there were inscribed circles on the faces of the dodecahedron whose centres were the centres of the faces and which were tangent to the edges of the dodecahedron (their centres would be the red points in the image above). Stereographic projection projects circles to circles and so in the regions of the plane above we would expect to see inscribed circles.

We know that these circles would be tangent to the sides at the projections of the points which lie halfway along each edge of the dodecahedron and on this basis I computed these circles. However, the outcome is this:

As you can see, the inner circles are indeed tangent to the sides of the regions. However, the outer regions' circles are rather messy and definitely do not lie in the regions. Why might this be?

To be explicit, to compute the locations of these circles on the plane:

1. For each face, I find three midpoints of edges on the outline of that face.
2. I project these midpoints onto the plane stereographically.
3. Three points define a circle and I compute this circle's centre and radius using the same idea as here. I'm fairly confident this last computation is bug-free and you can see that in the inner regions it does seem to be accurate.

Answer 1

I thought I'd just update everyone by saying that the comments precisely sorted out my problem: I had been projecting the vertices correctly and then for some reason assuming I could just draw straight lines between them. Instead, of course, the straight lines are in general projected to circular arcs and having sorted this out I got the interactive simulation to work. Here is an image:

and here is a link to the website where this projection is shown live where the controls are:

1. Rotate the dodecahedron around a horizontal axis by moving your mouse in the $x$-axis of the screen and rotate it around the vertical axis by moving your mouse in the $y$-axis of the screen.
2. Click and drag to rotate your viewpoint.
3. Middle-click (with your scroll-wheel) to pan your viewpoint.

On the blue plane are projected the edges and vertices (in orange) of the dodecahedron but also the projections of the incircles of each pentagonal face (in red) giving a live solution to the problem of finding a finite collection of circles in the plane such that each touch 5 others (discussed, for example, here). The red dots are the projections of the centres of the incircles on the sphere, showing how the centres of the circles are not preserved by the projection.