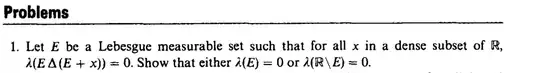Struggling with Problem 1, section 3.4 of Dudley's Real Analysis and Probability. The question asks us to prove the following statement:
Let E be a Lebesgue measurable set, such that for all x in a dense subset of $\mathbb{R}$, $\lambda (E\Delta (E+x)) =0$. Show that either $\lambda (E)$ or $\lambda(\mathbb{R}/E) =0$.
My thoughts so far: If x is such that the two sets E and E+x are fully disjoint, then naturally their symmetric difference is simply the union of the two sets, implying $\lambda (E) =0$.
However I'm struggling to show what happens if they are not disjoint! Any help would be much appreciated.