Fibonacci numbers, sum of squares and divisibility

Question

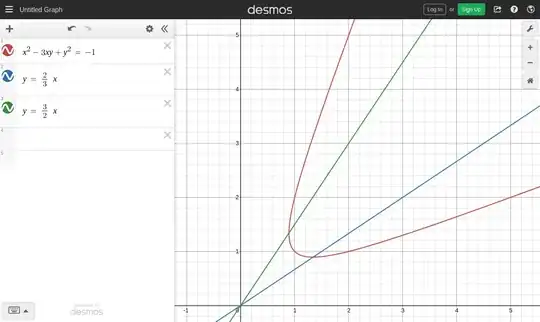
Let $(F_n)$ be the Fibonacci sequence (i.e. $F_{n+2} = F_{n+1}+F_n$ with $F_{-1}=1$ and $F_0=0$).

Consider $a,b \in \mathbb{Z}_{\ge 1}$ with $a \le b$, and $D=1+a^2+b^2$, such that $a$ and $b$ divide $D$.

Question: Must the ordered pair $(a,b)$ be equal to $(F_{2n-1},F_{2n+1})$ for some $n \ge 0$?

Remark: It was checked (by SageMath) for $b<10^5$.

Note that $F_{2n\pm1}$ divides $1+ F_{2n-1}^2 + F_{2n+1}^2$ thanks to the following identity:

Proposition: $1+ F_{2n-1}^2 + F_{2n+1}^2 = 3F_{2n-1}F_{2n+1}$.
proof: Apply Cassini's identity (below) with $2n$, then $F_{2n-1}F_{2n+1} = 1 + F_{2n}^2$. Now by definition, $F_{2n} = F_{2n+1} - F_{2n-1}$. Then $$ F_{2n-1}F_{2n+1} = 1 + (F_{2n+1} - F_{2n-1})^2 = 1 + F_{2n+1}^2 - 2F_{2n+1}F_{2n-1} + F_{2n-1}^2.$$ The result follows. $\square$

Cassini's identity: $F_{n-1}F_{n+1} = (-1)^n + F_n^2$.
proof: $F_{n-1}F_{n+1} - F_n^2 = \det \left(\begin{matrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{matrix} \right) = \det \left[\left(\begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right)^n \right] = \left[\det \left(\begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right) \right]^n = (-1)^n$. $\square$

Answer 1

Yes. This uses Vieta Jumping. Note first that your $\gcd(a,b) = 1,$ so that $ab| a^2 + b^2 + 1.$ Then $a^2 + b^2 + 1 = 3ab.$ Furthermore, the only Ground Solution, in the sense of Hurwitz 1907, is $(1,1).$ Every solution derives as a finite number of jumps from $1,1.$ That all solutions are Fibonacci numbers, two indices apart, may be proved by induction.

My way of dealing with this is closer to Hurwitz, and consists in looking at the hyperbola branch $x^2 - kxy + y^2 = -1 \; \; \; $ ($x,y>0$) and the location of any GrundLosung, which lie between lines $ y = \frac{k}{2} x$ and $ y = \frac{2}{k} x,$ showing by inequalities that there are no such points when $k \geq 4.$ Indeed, the entire arc on which fundamental solutions lies within $0 \leq x \leq 2, 0 \leq y \leq 2. \; $ The endpoints are $(x_1, y_1)$ and $(y_1, x_1)$ with $x_1 = \frac{2}{\sqrt{k^2-4}}$ and $$ y_1 = \frac{k}{\sqrt{k^2 - 4}} = \sqrt{1 + \frac{4}{k-2}} - \frac{2}{\sqrt{k^2-4}}$$ which is between $1$ and $2 \; . \; \;$ Furthermore, the arc does not pass through $(1,1)$ when $k \geq 4.$