Intuition of fundamental group in Hatcher

Question

I am reading the book Algebraic Topology by hatcher and more precisely the section about the fundamental group and have some questions about the intuition of the fundamental group. He starts this chapter with some intuitive examples on page 31 in the PDF (22 in the book). The setting he starts with is to imagine two circles in $\mathbb{R}^3$. He proceeds to consider one circle $A$ and a loop $B$ linking a multiple times. Two loops can then be added/multiplied in the usual way and he asks whether it is possible to continuously deform the sum of loops $B_1,B'_1$ to a loop that does not link $A$ at all.

Q1: In a more rigorous setting, am I understanding it correctly that he considers $\mathbb{R}^3 \setminus S^1$ or rather $\pi_1(\mathbb{R}^3 \setminus S^1, x_0)$ and inspects first, whether this fundamental group is trivial (which it is not, since on can just link the hole with another circle) and proceeds by inspecting whether the sum of loops can ever be $0$, meaning homotopic to a constant path? In the following picture that is taken from the book, one can see that $B_1 + B_{-1}$ can be deformed to $B_0$ which should be deformable to the constant path in $x_0$, right? (One pulls the piece of the loop that is in front of the circle behind the circle and then contracts it to $x_0$).

So what he is essentially saying is that, although two loops might be non trivial in $\pi_1$, it might be that their sum is trivial.

He proceeds to regard an example called the Borromean rings, where he "fixes $A,B$" and considers $C$ as a loop, meaning, if I understand it correctly, that the space is now $\mathbb{R}^3$ minus two circles. Again he asks, whether it is possible to deform $C$ to unlink it from $A,B$ or in other words to inspect whether the fundamental group of the space is trivial (more precisely he can conclude that it is not, when $C$ can't be deformed in this way).

He says that the loop $C$ goes forward through $A$, then forward through $B$, then backward through $A$ and backward through $B$, meaning we would have $1+1-1-1=0$ if we would give this process a representation in $\mathbb{Z}$. He justifies this phenomenon by saying that $C$ is not linked with $A$ and $B$ individually.

Q2:As far as I understand, he means here, that when "removing" $A$ or $B$ and only regarding the circle that is left and $C$, one would have a trivial loop, right? I am a bit irritated here. Is this related to the fact that $\pi_1$ needn't be abelian? As far as I can tell, this loop should not be trivial, however, if this represents the sum in $\mathbb{Z}$ it would be trivial. I suspect that this has something to do with another fundamental group other than $\mathbb{Z}$ underlying here, which might explain this.

Lastly, he now assumes that $A$ and $B$ are now linked and says that it is apparent that $C$ can be unlinked from $A$ and $B$ as in the following picture.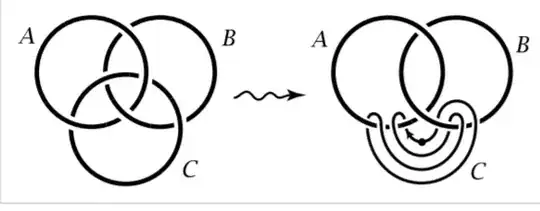

Q3: I may be overseeing something obvious, but I don't see how $C$ can be unlinked in any of the two pictures. If someone could explain it, I would be very grateful.

If I am missing something that he wanted to say in this section, I would also be greatful to learn about that. Thank you in advance!

Answer 1

Q1: Yes.

Q2: "Removing" loop $A$ means to fill it back in. So you are working in $\Bbb{R}^3 \smallsetminus B$; $A$ can no longer obstruct the homotopy taking $C$ to a point. With $A$ and $B$ both present, the path $C$ corresponds to a nontrivial commutator in the fundamental group, so this is giving an example of a nonabelian fundamental group. We could write it $aba^{-1}b^{-1}$ (if we were to go to the trouble of assigning orientations and specifying where on $C$ is the basepoint). When we "remove" $A$, the linking with $A$ becomes trivial, so in the new space with $A$ filled in, the path $C$ simplifies to $bb^{-1}$ which is trivial. A symmetric process occurs if we "remove" $B$ instead of $A$. Later, you will learn that the abelianization of the fundamental (homotopy) group is called the first homology group. In the homology group for $\Bbb{R}^3 \smallsetminus(A \cup B)$, the path $C$ is homologous to zero. One way to see that is that the abelianization is the fundamental group modulo all of its commutators, so the element corresponding to the path $C$ is trivial in the abelianization. So, yes, there is another group in play, the first homology group.

Q3: As drawn, the eye believes that the path $C$ bounds a twice-punctured disk, where points of $A$ are the punctures. If we can show that $C$ is the boundary of an unpunctured disk, then we can see that the path $C$ is homotopic to a point.

The path $C$ makes two sharp turns around $A$. Call the one on the left the "left turn" (which will never move in the following) and the one to its right the "right turn". Drag the right turn in the positive direction (anticlockwise) along $A$. Once the right turn is at the right-most point of $A$ you should see that $C$ no longer links $B$ at all. Continuing to move the right turn along $A$ in the positive direction, we eventually come around to just left of the left turn, and discover that $C$ bounds a disk. That disk is folded over $A$ like a towel on a towel rack.