As I read an algebraic topology book, I felt I knew exactly what the fundamental group is geometrically! I thought it counts the number of independent cycles. (my definition of dependence cycles (that may be incorrect): $\alpha,\beta$ are two dependent cycles if $\exists m,n\in\Bbb Z$ s.t. $\alpha^n=\beta^m$.)
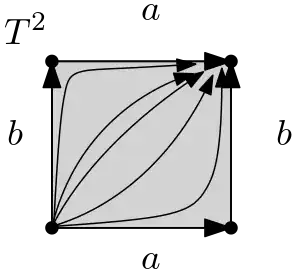
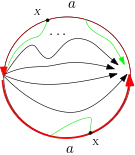
And according to this explanation it was always a serious question for me that why almost all authors compute the fundamental group of circle in very long way, some of them in a separate chapter and after proving many theorems instead of observing that there is only one independent cycle in circle! After these doubts, I read that $\pi_1(\Bbb RP^2)=\Bbb Z_2$. And here was the end of my dream. Since in term of my interpretation, the fundamental group is always free product of some $\Bbb Z$ but $\pi_1(\Bbb RP^2)=\Bbb Z_2$ is not in that form! So I want to know that
What does fundamental (homotopy) groups measure?
Isn't it true that if the space does not have a trivial loop, then it must contain at least one generator?
I think my interpretation is partially true but it ignores some information of the space. Or perhaps the missed point of my interpretation is that I don't consider the base point to be fixed.
The above interpretation also can be applied for $\pi_2$ (and $\pi_n$). i.e. $\pi_2$ counts the number of independent topological spheres (But in this case I don't know what is the independent topological spheres!!).