Prove that $\int_1^2 g(x^3 - 3x)\,\mathrm dx=\int_0^1 g(x^3 - 3x)\,\mathrm dx$

Question

Let $g:[-2, 2]\to\mathbb{R}$ be an even continuous function. Prove that $$\int_1^2g(x^3-3x)\,\mathrm dx=\int_0^1g(x^3-3x)\,\mathrm dx.$$

I found the following solution online, but I'm not sure why $$\int_0^1f(t)\,\mathrm d[x(t)]=\int_0^1 g(x^3-3x)\,\mathrm dx.$$ Also, why does $$\int_0^1g(t)\,\mathrm d[x(t)]=\int_{t=-1}^0 g(t)\,\mathrm d[y(t)]+\int_{t=-1}^0 g(t)\,\mathrm d[z(t)]\,?$$ Is it because $x(t) = -z(t)-y(t)$ and does $$\int_a^b\,\mathrm d(x(t))=-\int_a^b\,\mathrm d[y(t)]-\int_a^b\,\mathrm d[z(t)]\,?$$

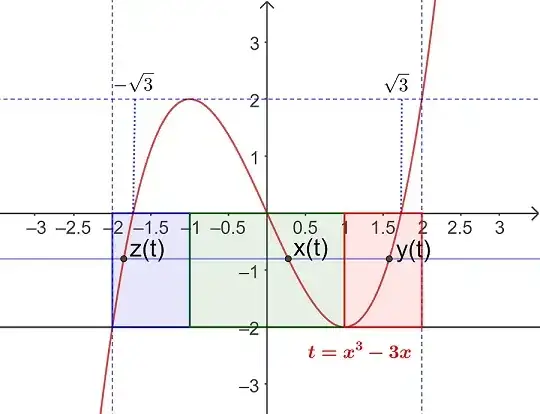
For each $t\in [-1,0]$, the equation $x^3-3x=t$ has three roots $x(t)\in[0,1]$, $y(t)\in[1,\sqrt3]$, $z(t)\in [-2,-\sqrt3]$.

By Vieta's Theorem, $x(t)+y(t)+z(t)=0$ $\forall$ $t$. Also, $x^3-3x$ is differentiable on $\mathbb{R},$ increasing in $(-2,-\sqrt{3}), $ decreasing in $[0,1],$ and increasing in $[1,\sqrt{3}],$ so by the inverse function theorem, $x,y,z$ are all differentiable for $t\in (-1,0).$ We then have

\begin{align*} \int_0^1 g(x^3-3x)\,\mathrm dx&=\int_0^{-1}g(t)\,\mathrm d[x(t)]\\ &= \int_{-1}^0 g(t)\,\mathrm d[y(t)]+\int_{-1}^0g(t)\,\mathrm d[z(t)]\\ &=\int_1^{\sqrt3} g(y^3 -3y)\,\mathrm dy+\int_{-2}^{-\sqrt3}g(z^3- 3z)\,\mathrm dz\\ &=\int_1^{\sqrt3} g(y^3-3y)\,\mathrm dy + \int_{\sqrt3}^2g(z^3 - 3z)\,\mathrm dz&\text{(as g is even)}\\ &=\int_1^2 g(x^3-3x)\,\mathrm dx \end{align*}

Answer 1

The approach presented by OP is clever and fine. It seems that just one aspect needs to be revised. Instead of $t\in[-1,0]$ we consider $t\in[-2,0]$. The graphic below might be helpful to better see what's going on.

                 

We see the red colored function \begin{align*} &h:[-2,2]\to\mathbb{R}\\ &h(x)=x^3-3x \end{align*} and observe the domain can be split into three intervals \begin{align*} [-2,2]=[-2,-1]\cup[-1,1]\cup[1,2] \end{align*} where the function $h$ has inverse functions denoted with $z=z(t), x=x(t)$ and $y=y(t)$. The rectangular regions of interest are colored in blue, green and red.

We want to show, given $g:[-2,2]\to\mathbb{R}$ an even, continuous function we have \begin{align*} \color{blue}{\int_{0}^{1} g(x^3-3x)\,dx=\int_{1}^{2} g(x^3-3x)\,dx}\tag{1} \end{align*}

In order to show (1) the idea is to use Vieta's formula applied to the zeros $x(t), y(t), z(t)$ of \begin{align*} h(x)-t = x^3-3x-t=0 \qquad\qquad t\in[-2,0]\tag{3} \end{align*} where the sum of the zeros is derived from the coefficient of $x^2$ in $h(x)-t$ which is equal to zero. \begin{align*} x(t)+y(t)+z(t)=0\qquad\qquad t\in[-2,0]\tag{2} \end{align*} When looking at the limits of integration in (1) we see that in $[0,1]\cup[1,2]$ only $x(t)$ and $y(t)$ are involved. But we can use that $g$ is an even function and split the interval $[1,2]=[1,\sqrt{3}]\cup[\sqrt{3},2]$. Since $g$ is even we consider $[-2,-\sqrt{3}]$ instead of $[\sqrt{3},2]$ and bring this way $z(t)$ into play so that (2) can be used conveniently.

We start with the right-hand side of (1) and obtain \begin{align*} \color{blue}{\int_{1}^{2}}&\color{blue}{g(x^3-3x)\,dx}\\ &=\int_{1}^{\sqrt{3}} g(x^3-3x)\,dx+\int_{\sqrt{3}}^{2} g(x^3-3x)\,dx\\ &=\int_{1}^{\sqrt{3}} g(x^3-3x)\,dx+\int_{-2}^{-\sqrt{3}} g(x^3-3x)\,dx\tag{3.1}\\ &=\int_{-2}^{0} g(t)\,dy(t)+\int_{-2}^{0} g(t)\,dz(t)\tag{3.2}\\ &=\int_{-2}^{0} g(t)\left(y^{\prime}(t)+z^{\prime}(t)\right)\,dt\\ &=-\int_{-2}^{0} g(t)x^{\prime}(t)\,dt\tag{3.3}\\ &=-\int_{1}^{0} g(x^3-3x)\,dx\tag{3.4}\\ &\,\,\color{blue}{=\int_{0}^{1} g(x^3-3x)\,dx} \end{align*} and the claim (1) follows

Comment:

• In (3.1) we use that $g$ is even.

• In (3.2) we substitute the inverse function $y=y(t)$ and $z=z(t)$.

• In (3.3) we use (2) and get by differentiation $x^{\prime}(t)+y^{\prime}(t)+z^{\prime}(t)=0$.

• In (3.4) we substitute back $x^3-3x=t$.

Answer 2

HINT:

Denote by $\phi(x) = x^3 - 3 x$. It is enough prove the equality $$\int_0^1 f(\phi(x)) d x = \int_1^2 f(\phi(x)) dx$$

for functions of form $\chi_{[-\epsilon, \epsilon]}$, where $\epsilon\in [0,2]$, and $\chi$ is a characteristic function, since every even integrable function can be approximated by linear combinations of such functions.

For every $t \in [-2,2]$, the equation $$\phi(x) = t$$ has three roots $$x(t) \le y(t) \le z(t)$$ with sum $0$ (Viete). Moreover, since $\phi$ is odd, we have $$(x(-\epsilon), y(-\epsilon), z(-\epsilon) )= (-z(\epsilon), - y(\epsilon), - x(\epsilon) )$$ see plot.

Let's evaluate LHS, RHS for the function $f= \chi_{[-\epsilon, \epsilon]}$. Note that $\chi_A \circ \phi = \chi_{\phi^{-1}(A)}$. Therefore

$$LHS = y(-\epsilon)$$

$$RHS = z(\epsilon) - z(-\epsilon) = z(\epsilon) + x(\epsilon)= - y(\epsilon) = y(-\epsilon)$$

so we have equality.