Image from Wikipedia
Put equally spaced points in a circle and label them 1,2,3,4,.. and so on. Connect 1 to 2, 2 to 4, 3 to 6 and generally $n$ to $2n$.
The intersection of these chords will form a cardioid as shown in the above picture.
Cardioids can also be made from rolling a circle over other and tracing this point.
Image from Wikipedia
Why doing these seemingly different things give the same result? How is these two operations related?
First, a bit of animated inspiration:
Now, we consider the origin-centered unit circle $\bigcirc O$, about which rolls unit circle $\bigcirc O'$. For $\theta$ the counter-clockwise direction angle of $\overline{OO'}$, we can define $P_\theta$ as the varying tangent point of the circles; $Q_\theta$ as the proverbial "spot of paint" point on $\bigcirc O'$ that traces the cardioid; and $R_\theta$ as the point of $\bigcirc O'$ from $O$, which traces a circle of radius $3$ about $O$. (Note that $P_0=Q_0=(1,0)$.) Let $T_\theta$ be the point where the extended segment $\overline{R_\theta Q_\theta}$ again meets the big circle, and let $S=(-3,0)$ be the fixed point on the far left of the big circle.
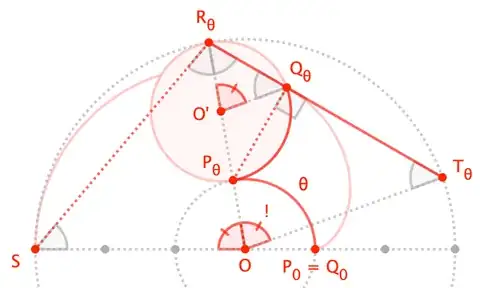
By the rolling definition of the cardioid locus, we know that $\angle P_\theta O P_0=\angle Q_\theta O' O$; equivalently, $\angle R_\theta OS = \angle Q_\theta O'R_\theta$ (as marked in the figure). Light angle-chasing through isosceles triangles tells us that $\angle T_\theta O S = 2\angle R_\theta O S$; thus, thinking clockwise from $S$, we see that $\overline{R_\theta T_\theta}$ is the precisely type of chord described in the definition of the cardioid as the envelope of chords.
"All we have to do", then, is show that chord $\overline{R_\theta, T_\theta}$ is tangent to the locus of $Q_\theta$. This takes a little Calculus.
The parametric form of our $Q_\theta$ (which, note, is shifted one unit right of the standard cardioid locus) is
$$Q_\theta = \left(\;1 + 2(1-\cos\theta)\cos\theta\;,\;2(1-\cos\theta)\sin\theta\;\right)$$ so the tangent vector has the form $$\overrightarrow{Q'_\theta} \;=\; \frac{d}{d\theta}Q_\theta \;=\; 2\;\left(\;-(1 - 2 \cos\theta) \sin\theta\;,\;(1 - \cos\theta) (1 + 2\cos\theta)\;\right)$$
Observe that, since $P_\theta=(\cos\theta,\sin\theta)$, we can calculate $$\overrightarrow{P_\theta Q_\theta}\;=\;Q_\theta-P_\theta \;=\;\left(\;(1 - \cos\theta) (1 + 2\cos\theta)\;,\; (1 - 2 \cos\theta) \sin\theta\;\right)$$ which amounts to the "negative reciprocal" of (half of) $\overrightarrow{Q'_\theta}$. The vectors are orthogonal. But $\overline{P_\theta Q_\theta}\perp\overline{R_\theta T_\theta}$ (by Thales), so it must be that $\overrightarrow{Q'_\theta}$ and $\overline{R_\theta T_\theta}$ are parallel; that is, the chord is indeed tangent to the locus, as desired. $\square$
The cardioid is a caustic, i.e. the envelope of all rays issued from a fixed point $P$ on a given circle $c$ (of centre $O$ and radius $r$) after their reflection on the circle itself. I'll find the properties of this envelope in a purely geometric way and show it is indeed a cardioid.
Take a point $A$ and a point $A'$ near to it, both on $c$. Let $s$ and $s'$ be the rays reflected of $PA$ and $PA'$, and $Q$ their intersection point. In the limit $A'\to A$, point $Q$ tends to some point $Q_0$: the envelope is the locus of all $Q_0$, as $A$ varies on the circle.
To find $Q_0$, observe first of all that $\angle AQA'=3APA'$ (see figure below). This is a simple matter of angle chasing: if $\alpha=\angle APA'$ and $\theta=\angle POA$, then $\angle PAQ=2\angle PAO=\pi-\theta$ and $\angle PMA=\theta-\alpha$, while $\angle AOA'=2\alpha$ and $\angle PA'Q=2\angle PA'O=\pi-\theta-2\alpha$. It follows that $$ \angle MQA'=\pi-\angle MA'Q-\angle QMA'= \pi-(\pi-\theta-2\alpha)-(\theta-\alpha)=3\alpha. $$
Consider now the circle $c'$ through $QAA'$, of radius $r'$, and arc $\gamma'=AA'$ on that circle. If $\gamma$ is the arc delimited by $A$ and $A'$ on circle $c$, then: $$ {\gamma'\over\gamma}= {2r'\cdot\angle AQA'\over 2r\cdot\angle APA'}= 3{r'\over r}. $$ In the limit $A'\to A$ circle $c'$ tends to a circle internally tangent to $c$, intersecting reflected ray $s$ at $Q_0$. In the same limit, we have $\gamma'/\gamma\to1$, because the ratio between an arc and the subtended chord tends to $1$ when the arc tends to zero; the above equality implies then $r'/r\to1/3$. Circle $c'$ tends then to the circle tangent to $c$ at $A$, having radius $r/3$ and centre $O'$. Point $Q_0$ is thus the intersection between this circle and the reflected ray $s$ (see figure below).
The internally tangent circle $i$ is also tangent to a circle with the same radius, concentric to $c$. Note that (by the converse of the intercept theorem) $\angle AO'Q_0=\angle BOA=\angle POO'$. Hence $Q_0$ can be thought of as a point "fixed" on circle $i$ ($Q_0=P$ when $\angle POO=0$) while $i$ rolls about the inner circle. This shows that its locus is indeed a cardioid.
In your case, you may check that a ray issued from point $0$ and hitting $c$ at point $n$ will be reflected to point $2n$: just remember that a ray hitting the circle at some point $A$ is reflected to a ray which is its reflection about line $OA$. Hence the reflected ray is tangent to the cardioid defined above.
