1

There's this nice Mathologer video showing how you can form a cardioid from multiples of $2$ mod $n$. So in the spirit of aspiration in mathematics I set a goal to put my new Manim tool to animate this thing.

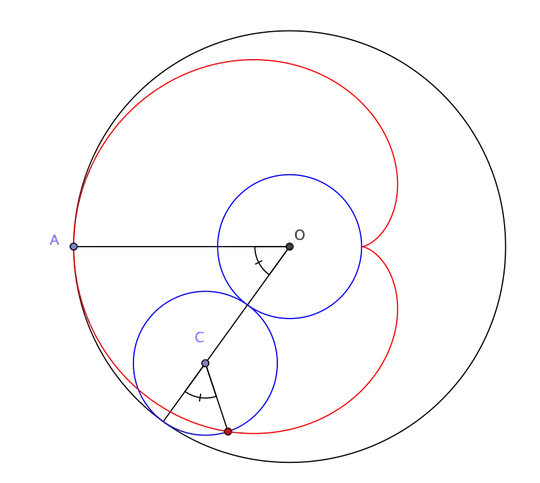
I've kind of succeeded(I could've created a hyperlink to my video if I had the knowledge for it) with a circle of radius $2.5\text{cm}$. Btw there's also a better illustration from a more competent Manim user.

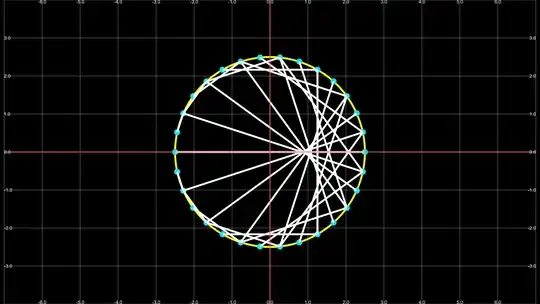
But as always the question shifts to $\textit{which cardioid is drawn exactly}$. For the circle radius of $2.5$ the plot looks like this:

enter image description here

$\uparrow n = 30(\text{also translates to number of dots})$

Now I want to know the exact description of that cardioid, at least which two circles would be used to trace it out(since that's what my final animation is supposed to be). At the moment, there's some (fortunate) symmetry on the x axis.

My idea is that if I know where the concave tip of that cardioid is, I'm home free. Because, then the distance from that point to the left intersection of the circle with the x axis is the diameter of the circle used to draw it and from there the parametrization is easy.

But where is that point?

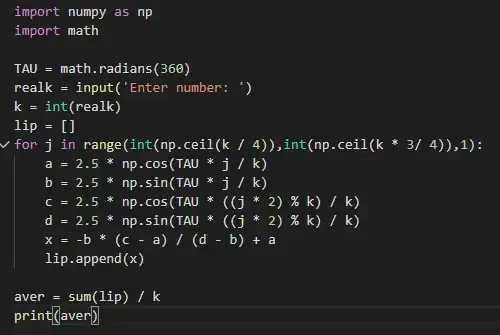
Guaranteed, it lies on the x axis so I need the x co-ordinate only. I tried to calculate it with a Python program to save myself time and it looks like this:

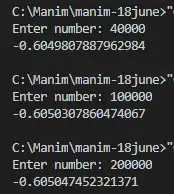
enter image description here

And the output looks very wrong like this:

enter image description here

Well of course I couldn't just pick any two lines that seem to pass through that point and say they intersect at the point of interest(or could I)? Point is, I have no idea. If there's uncertainty in the exact position of that point then maybe we're looking at an infinite series that could possibly have a clean looking answer. But as of now, I'm lost.

Any ideas?

Nεo Pλατo
  • 1,705

1 Answers1

1

As explained at the end of that video, this works because a cardioid is the caustic produced by rays from a source sitting on the circle itself, at the position of number zero (point $A$ in figure below), and reflected by the circle itself.

But it is not difficult to show that this cardioid is also a roulette, generated by a point on a circle having a radius which is $1/3$ that of the large circle, rolling on a circle of the same radius, concentric with the large circle. The initial position of the tracing point is the same as the position of the light source.

A proof of that can be found on Wikipedia, see here for a geometrical proof.

I don't know if this fully answers your question: feel free to ask for more details.

enter image description here

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77
  • So if I form the cardioid with two circles of radius 1/3 of the large circle I'm done – Nεo Pλατo Jul 03 '20 at 05:06
  • Because I found a way to indulge myself into integrals and got that x coordinate to be $\dfrac{10\tanh^{-1}\left(\dfrac{\tan \left(\dfrac{\pi}8 \right)}{\sqrt{3}}\right)}{\sqrt{3}}$ – Nεo Pλατo Jul 03 '20 at 05:14
  • But now that I have a clue of what's going on I'll plot my $\approx 0.89$ and your $\dfrac56$ and zoom in on them. And I'm not so fluent in Physics but what I can understand is that you can follow a line from 0 like a ray and show that it holds the laws of reflection as it goes, correct? – Nεo Pλατo Jul 03 '20 at 05:22
  • @NεoPλατo Yes, that is explained at the end of the video. I'm not sure I understand which x coordinate are you considering and how you computed it. – Intelligenti pauca Jul 03 '20 at 07:04
  • @NεoPλατo I've just seen that this is treated in full on Wikipedia: https://en.wikipedia.org/wiki/Cardioid#Cardioid_as_envelope_of_a_pencil_of_lines – Intelligenti pauca Jul 03 '20 at 07:45
  • What I did was consider a displacement of $\theta$ from $(1,0)$ and connect a line from it to the displacement of $2\theta$ from $(-1,0)$. This is because from the way I oriented the diagram $theta$ is at a value of $n\over2 + z$ for. some value z less that $n/4$. Then I deduced the x intercept of that line and did an average of it from $\frac{-\pi} 4 \le \theta \le \frac{\pi}4$ with an integral. I think I got the bounds wrong since I was doing all this while meditating on the problem as I went for a walk. – Nεo Pλατo Jul 03 '20 at 08:46