I took another look at my previous question on proving a certain trigonometric identity related to the braced heptagon: $$\sin\frac\pi7-\sin\frac{2\pi}7-\sin\frac{4\pi}7=-\frac{\sqrt7}2$$ Around the time I posted the first question I was trying to find similar identities for higher primes $p$ in the hope of bracing larger polygons, but without success. When I took the second look it became clear that such identities exist for all odd primes because of the quadratic subfield embedded in every cyclotomic field – the roots of unity naturally correspond with the edges of the polygon to be braced.
For example, with $p=11$ $$\frac{\sqrt{-11}-1}2=z+z^3+z^4+z^5+z^9\qquad z=e^{2i\pi/11}$$ and based on this I managed to find a cheap way to remove two degrees of freedom in a braced regular hendecagon using a Moser spindle:

This leads in turn to an explicit braced regular hendecagon with 41 vertices and 79 edges, much better than Khodulyov's 155. (The proof of rigidity is explained in the docstring of the function generating this graph in Shibuya.)
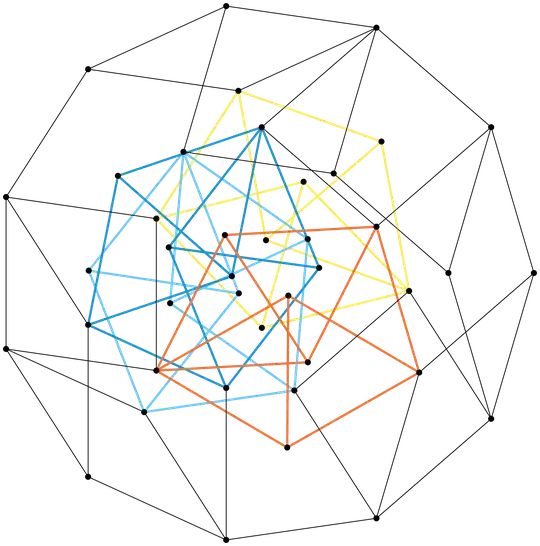
My question here concerns a pattern I noticed when finding the representations of $\sqrt{\pm p}$ in the integral basis of $\mathbb Q(\zeta_p)$, which is also a $\mathbb Q$-basis for the field (the sign is of course chosen to ensure containment).
#!/usr/bin/env python3
from sympy import *
x, zt = symbols('x zeta')
for p in (3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53):
quadratic = xx-p if p%4 == 1 else xx+p
zval = exp(2piI/p)
expr = x - factor(quadratic, extension=zval).args[1].subs(zval, zt)
print(f"p = {p}: \sqrt{{{x*x-quadratic}}} = {latex(expr)}\\")
No matter the $p$ two things seem to always hold:
- The coefficients in front of each $\zeta_p$ are always $2$, except the $\zeta^0$ coefficient which is $1$.
- If $p\equiv1\bmod4$ (so that we have $\sqrt{+p}$) the $\zeta$-powers occur in pairs $\zeta^i,\zeta^{-i}$. If $p\equiv3\bmod4$ (so that we have $\sqrt{-p}$) exactly one of $\zeta^i,\zeta^{-i}$ occurs for $1\le i\le\frac{p-1}2$.
To illustrate: $$p = 47: \sqrt{-47} = 2 \zeta^{21} + 2 \zeta^{18} + 2 \zeta^{17} + 2 \zeta^{16} + 2 \zeta^{14} + 2 \zeta^{12} + 2 \zeta^{9} + 2 \zeta^{8} + 2 \zeta^{7} + 2 \zeta^{6} + 2 \zeta^{4} + 2 \zeta^{3} + 2 \zeta^{2} + 2 \zeta + 1 + \frac{2}{\zeta^{5}} + \frac{2}{\zeta^{10}} + \frac{2}{\zeta^{11}} + \frac{2}{\zeta^{13}} + \frac{2}{\zeta^{15}} + \frac{2}{\zeta^{19}} + \frac{2}{\zeta^{20}} + \frac{2}{\zeta^{22}} + \frac{2}{\zeta^{23}}\\ p = 53: \sqrt{53} = 2 \zeta^{26} + 2 \zeta^{23} + 2 \zeta^{22} + 2 \zeta^{21} + 2 \zeta^{20} + 2 \zeta^{19} + 2 \zeta^{18} + 2 \zeta^{14} + 2 \zeta^{12} + 2 \zeta^{8} + 2 \zeta^{5} + 2 \zeta^{3} + 2 \zeta^{2} + 1 + \frac{2}{\zeta^{2}} + \frac{2}{\zeta^{3}} + \frac{2}{\zeta^{5}} + \frac{2}{\zeta^{8}} + \frac{2}{\zeta^{12}} + \frac{2}{\zeta^{14}} + \frac{2}{\zeta^{18}} + \frac{2}{\zeta^{19}} + \frac{2}{\zeta^{20}} + \frac{2}{\zeta^{21}} + \frac{2}{\zeta^{22}} + \frac{2}{\zeta^{23}} + \frac{2}{\zeta^{26}}$$
Are the two observations above true for all odd primes $p$? If so, how can they be proved?