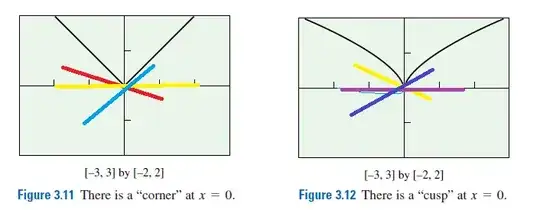
We know that a derivative fails at cusp or corner. As we know a corner is where you have two distinct tangent lines and a cusp is where you have one tangent line which is vertical. I realized that a cusp and corner can have infinitely many tangent lines. See the image below of what I mean. I draw vertical lines at the corner and cusp. The first left graph is $y = |x|$ and the the right graph is $y = x^{2/3}$. I am confused. Perhaps I do not understand what a tangent line really is. Can you explain the flaw of my logic? Thanks!
-
4It's all a question of how you define tangent. – Gerry Myerson Oct 11 '21 at 03:01
-
2Consider this: Can someone provide the formal definition of the tangent line to a curve? Or this: Problem with basic definition of a tangent line. Or this: What characterizes a tangent line? – David K Oct 11 '21 at 03:11
-
2We don't actually know there are any tangents at a corner or cusp until we know what a tangent is. Whoever told you there are two tangents, what was their definition? That would be a useful starting point to investigate. – David K Oct 11 '21 at 03:15
-
I was trying to understand what a cusp and corner is on Math Stack Exchange. Here it is https://math.stackexchange.com/questions/2429089/cusp-vs-corner-or-both – Deadpool 36701 Oct 12 '21 at 17:30
1 Answers
Clarification: in either example, at the corner or the cusp, the tangent line is not defined. You have to go back to the definition of the derivative, which is the name of the slope of the tangent line.
You begin by writing down the slope of the secant line connecting the point $(0, 0)$ and a nearby point $\bigl( h, f(h) \bigr)$ on the graph of the function $f$. Imagine that $h$ is very small, but could b either positive or negative, as we’re about to ask what happens to the slope in the limit as $h$ goes to $0$. The slope, which depends on $h$ is $$ m = \frac{\Delta y}{\Delta x} = \frac{f(h) - f(0)}{h - 0} = \frac{f(h)}{h}. $$
Now, to obtain the derivative, we ask what this quantity approaches as $h \to 0$. (Notice that you can’t just plug in $h=0$.) In each of your two examples, this limit does not exist, so the derivative does not exist, so we say that the function is not differentiable at $x=0$. But the issue is slightly different in each case.
Corner: $f(x) = \lvert x \rvert$. Here, you find that for $h>0$, the slope is $m=1$ (independent of the magnitude $h$), but for $h<0$, we have $m=-1$. So, no matter how small we make $h$ in magnitude, these two values remain apart. In notation, $$ \lim_{h \to 0^+} \frac{f(h)}{h} = +1 \neq -1 = \lim_{h \to 0^-} \frac{f(h)}{h} \quad \Longrightarrow \quad f’(0) = \lim_{h \to 0^+} \frac{f(h)}{h} \text{ does not exist}. $$
Cusp: $f(x) = \lvert x \rvert^{2/3}$. Here you find that for $h>0$, the slope is $m = h^{-1/3}$, a quantity that grows (positively) without bound as $h$ vanishes. On the other hand, for $h<0$, we have $m = -h^{-1/3}$, which grows (negatively) without bound. In limit notation, $$ \lim_{h \to 0^+} \frac{f(h)}{h} = +\infty \neq -\infty = \lim_{h \to 0^-} \frac{f(h)}{h} \quad \Longrightarrow \quad f’(0) = \lim_{h \to 0^+} \frac{f(h)}{h} \text{ does not exist}. $$
By the way, it might be useful to go through this process with a function such as $f(x) = x^2 + x$ at $x=0$, where the limit does exist, so the slope of the tangent line is well-defined $(m=1)$.
- 25,273