3

Problem:

Prove $$\cot^{-1}(\tan 2x)+\cot^{-1}(-\tan 3x)=x$$

My proof:

$$\begin{align}\text{L.H.S}&=\cot^{-1}(\tan 2x)+\cot^{-1}(-\tan3x) \\ &=\cot^{-1}(\cot (\frac{\pi}{2}-2x))-\cot^{-1}(\cot(\frac{\pi}{2}-3x))\\ &=3x-2x\\ &=x\\ &=\text{R.H.S(proved)}\end{align}$$

Will my proof still be valid if $2x$ or $3x$ is in any quadrant other than the 1st quadrant? What will be the correct proof that will hold true for any quadrant? Is this identity only true when 2x & 3x are in the first quadrant?

tryingtobeastoic
  • 3,176

1 Answers1

1

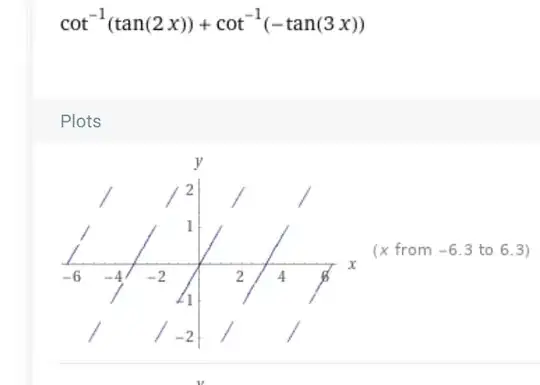
Good question about whether your proof applies when $2x$ is outside the first quadrant.

In fact, your proof applies only when you define $\mathrm{arccot}$'s principal range as $\left(-\frac{\pi}2,0\right)\cup\left(0\frac{\pi}2\right]$ and both $\left(\frac\pi2-2x\right)$ and $\left(\frac\pi2-3x\right)$ are within this range.

Furthermore, the given statement is actually not identically true, whichever of the two contrasting definitions of $\mathrm{arccot}$ we choose.

  1. Let us define $\textrm{arccot}$'s principal range to be $(0,\pi).$ Then $$\text{LHS}=\mathrm{arccot}(\tan 2x)+\mathrm{arccot}(-\tan3x)\\ =\frac {\pi}2-\arctan(\tan 2x)+\left(\frac {\pi}2-\arctan(-\tan 3x)\right)\\ =\pi+\arctan(\tan 3x)-\arctan(\tan 2x)\\ =\pi+(3x+m\pi)-(2x+n\pi)\quad\text{for some }m,n \\ =x+k\pi\quad\text{for some }k.$$

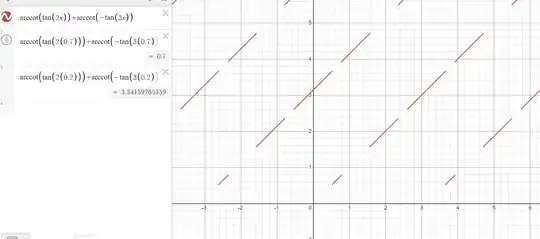
    enter image description here

    For example, $$x=0.7\implies\text{LHS}=0.7=x=\text{RHS},$$ but $$x=0.2\implies\text{LHS}=0.2+\pi\neq x=\text{RHS}.$$

  2. On the other hand, if we define $\textrm{arccot}$'s principal range to be $\left(-\frac{\pi}2,0\right)\cup\left(0\frac{\pi}2\right],$ LHS still doesn't identically equal $x:$

    enter image description here

ryang
  • 38,879
  • 14
  • 81
  • 179
  • 1
    To repeat my remark from yesterday: If possible, switch to another textbook. – ryang Sep 22 '21 at 07:30
  • It's not possible, unfortunately. – tryingtobeastoic Sep 22 '21 at 12:57
  • 1
    @tryingtobeastoic That's too bad. That you're reading it critically is more important anyway. Keep it up. – ryang Sep 22 '21 at 13:19
  • I think you missed a thing. My proof only applies when we pick the 1st definition of $arccot$, and when $\frac{\pi}{2}-2x$ and $\frac{\pi}{2}-3x$ are in the 1st quadrant. If these two angles are in the 4th quadrant, my proof doesn't work. If the mentioned angles are in the 4th quadrant, the 2nd line of my proof would become... – tryingtobeastoic Sep 23 '21 at 06:24
  • $$\cot^{-1}(-\cot (\frac{\pi}{2}-2x))-\cot^{-1}(-\cot(\frac{\pi}{2}-3x))$$

    $$-\cot^{-1}(\cot (\frac{\pi}{2}-2x))+\cot^{-1}(\cot(\frac{\pi}{2}-3x))$$

    $$-x$$

     – tryingtobeastoic Sep 23 '21 at 06:27
  • What do you think? – tryingtobeastoic Sep 23 '21 at 06:31
  • But $\cot^{-1}(x)$ is only an odd function according to WolframAlpha's definition. So, how can my 2nd line be accurate according to desmos's definition, where I treated $\cot^{-1}()$ as an odd function? – tryingtobeastoic Sep 23 '21 at 06:56
  • @tryingtobeastoic Ah okay, I just edited the Answer to reflect the fact that if you're using definition two (Desmos's), then yes your proof is simply invalid. Re: you new comments: 1. it's about actual angle values, not quadrants. 2. your original proof actually works under defn one and when $\left(\frac\pi2-2x\right)$ and $\left(\frac\pi2-3x\right)$ are both in, say, -89 to -1 degs (but NOT in, say, 271-359 degs). 3. your new attempt is invalid because (a) it is incorrect to add the minus signs when taking complementary angles, (b) the LHS ought to be still be of the form "$x+k\pi$". – ryang Sep 23 '21 at 07:41
  • I understand. I assumed $(\frac{\pi}{2}-2x)$ & $(\frac{\pi}{2}-3x)$ to be in the fourth quadrant, and considered $2x$ & $3x$ to be acute angles, and then I tried to apply the method mentioned in this question. However, $(\frac{\pi}{2}-2x)$ & $(\frac{\pi}{2}-3x)$ can never be in the fourth quadrant if $2x$ & $3x$ are acute. One of my presuppositions is invalid. That's why I am wrong in my new attempt. – tryingtobeastoic Sep 23 '21 at 12:25
  • I couldn't thank you yesterday for helping me greatly! Thank you!!!!!!! By the way, I posted a question based on our discussion yesterday. If you want, you can check it out! – tryingtobeastoic Sep 24 '21 at 04:22