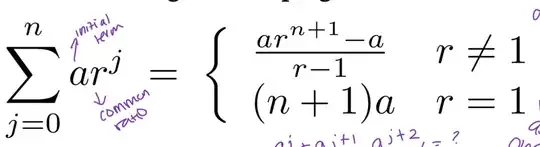So for, the above formula, how did they get $(n+1)$ a for the geometric progression when $r = 1$. I also am confused where the negative a comes from in the following sequence of steps.
-
Welcome to Mathematics SE. Take a tour. You'll find that simple "Here's the statement of my question, solve it for me" posts will be poorly received. What is better is for you to add context (with an edit): What you understand about the problem, what you've tried so far, etc.; something both to show you are part of the learning experience and to help us guide you to the appropriate help. You can consult this link for further guidance. – person Sep 20 '21 at 17:21
-
If $r=1$, then you have $n+1$ time $a+a+a+\cdots +a$. This implies $\sum=a(n+1)$. – lone student Sep 20 '21 at 17:28
-
There are $n+1$ terms in $\sum_{k=0}^n.$ – Thomas Andrews Sep 20 '21 at 17:29
-
The second question is unclear, because you didn’t give us the left hand side of the equality. We can guess, but … – Thomas Andrews Sep 20 '21 at 17:30
2 Answers
When $r=1$ we have
$$S_{n}=\sum_{j=0}^{n}ar^{j}=\sum_{j=0}^{n}a=\underbrace{a+a+a+...+a+a}_{(n+1)-\text{times}}=...$$
For $r\neq 1$, let
$$S_{n}=\sum_{k=0}^{n}ar^{k}=a+ar+ar^{2}+...+ar^{n-1}+ar^{n}$$
Multiplying by $r$ we have
$$rS_{n}=\sum_{k=0}^{n}ar^{k+1}=ar+ar^{2}+ar^{3}+...+ar^{n}+ar^{n+1}$$
Then which terms cancel when we compute $rS_{n}-S_{n}$?
Or adding and subtracting the term $a$ to the RHS of $rS_{n}$ we have
$$rS_{n}=\color{red}{a}+ar+ar^{2}+ar^{3}+...+ar^{n}+ar^{n+1}-\color{red}{a}$$ $$=\left(a+ar+ar^2+...+ar^{n}\right)+ar^{n+1}-a$$
and what is the term in the brackets equal to?
- 10,599
Consider the sum $$\sum_{j=0}^{\infty}ar^j$$.
Now for find the sum we need show that the sequence of partial sum of the series converges.
Let us consider the partial sum of the serie $$S_n=a+ar+ar^2+ar^3+\cdots ar^n$$
Consider $$rS_n=ar+ar^2+ar^3+\cdots ar^{n+1}$$
Now $$S_n-rS_n=a-ar^{n+1}\iff S_n(1-r)=a-ar^{n+1}$$
For $r\neq 1$ $$S_n=\frac{a-ar^{n+1}}{1-r}$$
Now $S_n$ is the $n$-th partial sum of your serie, for find the sum is sufficient take $\lim_{n\to \infty }S_n$ and if it exists to a number $s$ we say that the sum of the serie is $s$. But what can you say about
$$\lim_{n\to \infty} \frac{a-ar^{n+1}}{1-r}$$
what can you infer from $r$ for the limit exists?
In the case of the above limit exists then $$\sum_{j=0}^{\infty}ar^{j}=s$$
- 776