Evaluation of ${\sum\limits_{\Bbb N} (\text {ker}(x)+i\text{kei(x)})=\sum\limits_1^\infty \text K_0\left(\sqrt ix\right)= 0.133691… - 0.7256312… i}$?

Question

$\large \text{Introduction:}$

This summation is related to this other Bessel Summation question:

$$\mathrm{\sum\limits_{-\infty}^\infty Ai(x)=1}\ \text{and}\ \sum\limits_{-\infty}^0 \mathrm{Bi(x)}$$

$\large \text{Goal Sum:}$

The actual question uses the Modified Bessel Function of the Second Kind and corresponding Kelvin functions The sum may have a slightly different value. It would probably be easiest to use integral representations as alternative forms of the functions may not work well. I am looking for 2 solutions: one closed form for the kei(x) sum and one closed form for the ker(x) sum. This is because all other summations of just a function ended up with a closed form. Also try contour representations of which I am unfamiliar:

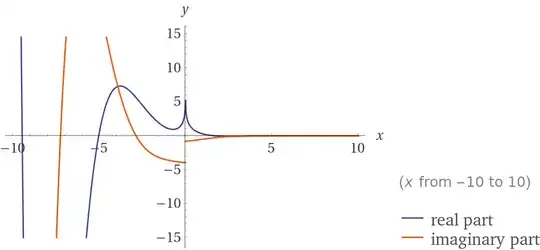
$${\sum_{\Bbb N} \text{ker}(x)+i\text{kei}(x)= \sum_1^\infty \text K_0\left(\sqrt ix\right)= \sum_{x=1}^\infty \int_0^\infty \frac{\cos\left(\sqrt{i}tx\right)}{\sqrt{t^2+1}}dt=\sum_{x=1}^\infty\int_0^\infty \cos\left(\sqrt ix\sinh(t)\right)dt=0.133691752819604391549325780771600891… - 0.725631207729182631737443031218031025… i}$$

Here is a summand plot. Note the sum starts for $x\ge 1$:

$\large \text{Abel-Plana Integral Representation:}$

Another method is to use the Abel-Plana formula which does work as shown here with the difference term evaluated. The simpler integral over the summand only has a complicated closed form. Here the integral of the summand in the last step can be found by evaluating the closed form antiderivative from $[-1,\infty]-[-1,1]$:

$${\sum_0^\infty \text{ker}(x+1)+i\ \text{kei}(x+1) =\frac{\text{ker}(1)+i \ \text{kei}(1)}{2}+\int_0^\infty \text {ker}(x+1)+i\ \text{kei}(x+1) dx+\int_0^\infty \frac{i\ \text{ker}(1-ix)-\ \text{kei}(1-ix)-i\ \text{ker}(1+ix)+\ \text{kei}(1+ix)}{e^{2\pi x}-1}dx=\frac12 \text K_0\left(\sqrt i\right)+\int_0^\infty \text K_0\left(\sqrt i(x+1) \right)dx +i\int_0^\infty \frac{\text K_0\left(\sqrt i(1-ix) \right)-\text K_0\left(\sqrt i(1+ix) \right)}{e^{2\pi x}-1}dx}$$

$\large \text{Other Integral Representations:}$

Using @Jack Barber’s Floor function integral solution in the following question gives this result. Please see the bolded “Kelvin functions” link for more Generalized Kelvin function information:

Evaluation of $$\sum_{x=0}^\infty \text{erfc}(x)$$

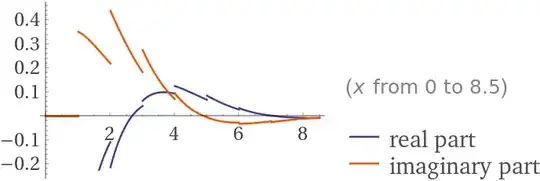
$$\sum_\Bbb N(\text{ker(x)}+ i\text{kei}(x))=\sum_\Bbb N \text K_0\left(\sqrt i x\right) =\sqrt[4]{-1}\int_0^\infty\lfloor x\rfloor \text{kei}_1(x)dx+\sqrt[-4]{-1}\int_1^\infty \lfloor x\rfloor \text{ker}_1(x)dx=(-1)^{-\frac34}\int_1^\infty \lfloor x\rfloor \text K_1\left(\sqrt[4]{-1} x\right)dx$$

Here is the integrand plot:

Let’s now use the Fractional Part/Sawtoothwave function. Note that the point discontinuities can be ignored as a result of the integral operator:

$$\text{frac}(x)=\mod{(x,1)}=\text{sawtoothwave}(x)=\boxed{\{x\}}=x-\lfloor x\rfloor\implies x-\{x\}=\lfloor x\rfloor$$

Therefore our goal sum can be expressed as the following. This is the closed form integral of $x\text{kei}_1(x),x\text{ker}_1(x)$. The integral on $[1,\infty]$ is the same as on $[0,\infty]-[0,1]$, but the integral of the $x\text{ker}_1(x)$ function integral on $[0,\infty]$ is just $-\frac\pi 2$ while for $x\text{ker}_1(x)$, it is just $0$ on the same interval meaning that:

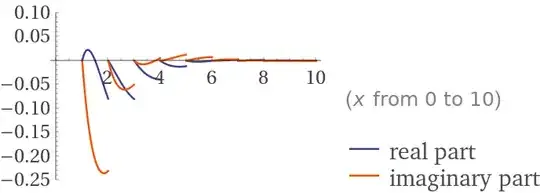
$$\sum_1^\infty (\text{ker}(x)+i\text{kei}(x))= \sqrt[4]{-1}\int_0^\infty (x-\{x\}) \text{kei}_1(x)dx+\sqrt[-4]{-1}\int_1^\infty (x-\{x\}) \text{ker}_1(x)dx = (-1)^{-\frac34}\left(\frac\pi 2+\int_0^1 x \text{kei}_1(x)dx+\int_1^\infty\{x\} \text{kei}_1(x)dx \right)+ (-1)^{\frac 34}\left(\int_0^1 x \text{ker}_1(x)dx+\int_1^\infty\{x\} \text{ker}_1(x)dx \right) $$

$$\sum\limits_1^\infty \text K_0\left(\sqrt ix\right) = (-1)^{-\frac34}\int_1^\infty (x-\{x\})\text K_1\left(-\sqrt[4]{-1} x\right)dx =\sqrt[4]{-1}\left(\frac{i\pi}2+\int_0^1x \text K_1\left(\sqrt[4]{-1} x\right)+\int_1^\infty\{x\}\text K_1\left(\sqrt[4]{-1} x\right)dx\right)$$

There are many alternate forms for the floor function, so many more integral representations are possible in terms of related functions.

Here is a plot of that Fractional Part function times the Bessel-Kelvin type function integrand:

$\large \text{Conclusion:}$

Note that I could have made a typo. An exact form answer is needed and a closed form is optional. This question was found as the summand graph decreases rapidly and after a lot of terms, and converges quickly to over $50$ digits in just the first $300$ terms. We now have $2$ working integral representations of the constant, so how can we evaluate them or the sum representations? Please correct me and give me feedback!

Note that $\sqrt[-2]2=\frac1{\sqrt 2} $ is easier for MathJax $From @Yuri’s help, here is an integral representation for:

$$\sum_\Bbb N \text{ker}(x)=\int_0^\infty \frac{e^{\cosh(x)\sqrt[-2]2} \cos(\cosh(x) \sqrt[-2]2)}{\big(e^{\cosh(x) \sqrt[-2]2} \cos(\cosh(x) \sqrt[-2]2) - 1\big)^2 + e^{\sqrt2\cosh(x)} \sin^2(\cosh(x) \sqrt[-2]2)} - \frac 1{\big(e^{\cosh(x) \sqrt[-2]2} \cos(\cosh(x) \sqrt[-2]2) - 1\big)^2 + e^{\sqrt2 \cosh(x)} \sin^2(\cosh(x) \sqrt[-2]2)}dx $$

$$\sum_\Bbb N \text{kei}(x)=-\int_0^\infty \frac{e^{\cosh(x)\sqrt[-2]2} \sin(\cosh(x) \sqrt[-2]2)}{\big(e^{\cosh(x) \sqrt[-2]2} \cos(\cosh(x) \sqrt[-2]2) - 1\big)^2 + e^{\sqrt2 \cosh(x)} \sin^2(\cosh(x) \sqrt[-2]2)} dx$$

Answer 1

To evaluate \begin{equation} S=\sum_{n=1}^\infty K_0(n\sqrt{i}) \end{equation} we can use the Mellin transform \begin{equation} \int_{0}^{\infty}t^{s-1}K_0\left(t\right)\,dt=2^{s-2}\Gamma \left(\frac{s}{2}\right)^2 \end{equation} ($\Re s>0$) to write \begin{equation} K_0(n\,e^{i\pi/4})=\frac{1}{2i\pi}\int_{c-i\infty}^{c+i\infty}2^{s-2}\Gamma\left(\frac{s}{2}\right)^2(n\,e^{i\pi/4})^{-s}\,ds \end{equation} with $\Re c>0$. Then, by choosing $c>1$, on may express \begin{align} S&=\frac{1}{2i\pi}\sum_{n=1}^\infty \int_{c-i\infty}^{c+i\infty}2^{s-2}\Gamma\left(\frac{s}{2}\right)^2e^{-is\pi/4}n^{-s}\,ds\\ &=\frac{1}{2i\pi}\int_{c-i\infty}^{c+i\infty}2^{s-2}\Gamma\left(\frac{s}{2}\right)^2\zeta(s)e^{-is\pi/4}\,ds \end{align} by changing the order of integration and summation. To evaluate the integral, one can close the contour with a semi-large circle on the left in the complex plane. It can be shown that the contribution of this part of the contour vanishes as the radius tends to infinity. The poles of the function $f(s)=2^{s-2}\Gamma\left(\frac{s}{2}\right)^2\zeta(s)e^{-is\pi/4}$ are situated at $s=1$ (simple) and $s=-2p$ (double) with $p=0,1,2,\cdots$. The calculation of the residues poses no difficulties: \begin{align} \operatorname{Res}\left( f(s),s=1 \right)&=\frac{1-i}{2\sqrt{2}}\pi\\ \operatorname{Res}\left( f(s),s=0 \right)&=\frac\gamma2+i\frac{\pi}{8}-\ln2-\frac{\ln\pi}{2}\\ \operatorname{Res}\left( f(s),s=-2p \right)&=\frac{e^{ip\pi/2}}{2^{2p}}\frac{\zeta'(-2p)}{(p!)^2} \end{align} where $p\ge1$ is an integer. The expression for the derivative of the zeta function at the negative even integers is see here \begin{equation} \zeta'(-2p)=\frac{(-1)^p (2 p)!}{2^{2p+1}\pi^{2p}}\zeta(2p+1) \end{equation} We obtain then \begin{equation} S=\frac{1-i}{2\sqrt{2}}\pi+\frac\gamma2+i\frac{\pi}{8}-\ln2-\frac{\ln\pi}{2}+\sum_{p=1}^\infty\frac{(-1)^pe^{ip\pi/2}}{2^{2p}}\frac{ (2 p)!}{(p!)^2}\frac{\zeta(2p+1)}{2^{2p+1}\pi^{2p}} \end{equation} which can be written as \begin{equation} S=\frac{\gamma}{2}-\ln \left(2\right)-\frac{\ln \left(\pi \right)}{2}+\frac{i \pi}{8}+\frac{\sqrt{-i}}{2}\pi+\frac12\sum_{p=1}^\infty\left(-i\right)^{p} \binom{2 p}{p} \frac{\zeta \left(2 p+1 \right)}{\left(4 \pi \right)^{2 p}} \end{equation} which converges faster than the initial Bessel function series. On have then \begin{align} \sum_{n=1}^\infty\operatorname{ker}(n)&=\frac{\gamma}{2}-\ln \left(2\right)-\frac{\ln \left(\pi \right)}{2}+\frac{\pi}{2\sqrt{2}}+\frac12\sum_{q=1}^\infty\left(-1\right)^{q} \binom{4q}{2q} \frac{\zeta \left(4q+1 \right)}{\left(4 \pi \right)^{4q}}\\ \sum_{n=1}^\infty\operatorname{kei}(n)&=\frac{ \pi}{8}-\frac{\pi}{2\sqrt{2}}+\frac12\sum_{q=1}^\infty\left(-1\right)^{q} \binom{4q-2}{2q-1} \frac{\zeta \left(4q-1 \right)}{\left(4 \pi \right)^{4q-2}} \end{align} To go further, one could expand the zeta function in series and change the order of summation: \begin{align} J&=\sum_{p=1}^\infty\left(-i\right)^{p} \binom{2 p}{p} \frac{\zeta \left(2 p+1 \right)}{\left(4 \pi \right)^{2 p}}\\ &=\sum_{p=1}^\infty \binom{2 p}{p} \frac{\left(-i\right)^{p}}{\left(4 \pi \right)^{2 p}}\sum_{n=1}^\infty\frac{1}{n^{2p+1}}\\ &=\sum_{n=1}^\infty\sum_{p=1}^\infty \binom{2 p}{p} \frac{\left(-i\right)^{p}}{\left(4 \pi \right)^{2 p}}\frac{1}{n^{2p+1}} \end{align} by denoting \begin{equation} X=\frac{-i}{16\pi^2n^2} \end{equation} we have $\left|X\right|<1/4$ and by using the classical generating function for the central binomial coefficient \begin{align} J&=\sum_{n=1}^\infty\frac{1}{n}\sum_{p=1}^\infty\binom{2 p}{p}X^p\\ &=\sum_{n=1}^\infty\frac{1}{n}\left[\frac{1}{\sqrt{1-4X}}-1\right]\\ &=\sum_{n=1}^\infty\frac{1}{n}\left[\frac{1}{\sqrt{1+\frac{i}{ 4\pi^2n^2}}}-1\right]\\ &=\sum_{n=1}^\infty\left[\frac{2\pi}{\sqrt{4\pi^2n^2+i}}-\frac{1}{n}\right] \end{align} and thus \begin{equation} S=\frac{\gamma}{2}-\ln \left(2\right)-\frac{\ln \left(\pi \right)}{2}+\frac{i \pi}{8}+\frac{\sqrt{-i}}{2}\pi+\frac12\sum_{n=1}^\infty\left[\frac{2\pi}{\sqrt{4\pi^2n^2+i}}-\frac{1}{n}\right] \end{equation} This expression could probably be established using a Poisson summation technique, as it is similar to a summation of the Fourier cosine transform of the Bessel function. It can be deduced from the identity (8.526.1) of Gradshteyn & Ryzhik. Its convergence is however much slower, but it does not involve special functions.

By extracting the real and imaginary parts of this expression, one obtains \begin{align} \sum_{n=1}^\infty\operatorname{ker}(n)&=\frac{\gamma}{2}-\ln \left(2\right)-\frac{\ln \left(\pi \right)}{2}+\frac{\pi}{2\sqrt{2}}+\frac\pi{\sqrt2}\sum_{n=1}^\infty\left[\frac{ \sqrt{\sqrt{16 \pi^{4} n^{4}+1}+4 \pi^{2} n^{2}}}{\sqrt{16 \pi^{4} n^{4}+1}}-\frac1n\right] \\ \sum_{n=1}^\infty\operatorname{kei}(n)&=\frac{ \pi}{8}-\frac{\pi}{2\sqrt{2}}-\frac\pi{\sqrt2}\sum_{n=1}^\infty\frac{ \sqrt{ \sqrt{16 \pi^{4} n^{4}+1}-4 \pi^{2} n^{2}}}{\sqrt{16 \pi^{4} n^{4}+1}} \end{align}

Answer 2

Is known the representation $$K_0(z)=\int\limits_0^\infty e^{-z\cosh t}\,\text dt,\qquad \left(|\arg z|<\dfrac\pi2\right).\tag1$$

Then $$I=\sum\limits_{k=1}^\infty K_0\left(\sqrt i k\right) =\int\limits_0^\infty\sum\limits_{k=1}^\infty e^{-\sqrt i\,k\cosh t}\,\text dt =\int\limits_0^\infty\dfrac{e^{-\sqrt i\cosh t}}{1-e^{-\sqrt i\cosh t}}\,\text dt =\int\limits_0^\infty\dfrac{\text dt}{e^{\frac1{\sqrt2}(1+i)\cosh t}-1},$$ $$I=\dfrac12\int\limits_{-\infty}^\infty\dfrac{\text dt}{e^{\frac1{\sqrt2}(1+i)\cosh t}-1},\tag2$$ with the numeric value

wherein calculating in the bounds $(-6,6)$ provides more than $\,50\,$ right digits.

Analysis shows, that the best way to calculate the integral $(2)$ is the numeric one.

Really, the substitution $\,t=\dfrac{13}{10}\,$ leads to the representation $$I=\dfrac{13}{20}\int\limits_{-\infty}^\infty\dfrac{\text dz}{e^{\frac{1+i}{\sqrt2}\cosh\frac{13}{10}z}-1},\tag3$$ which contains the factor $e^{-z^2}.$

This allows to use the Hermite's quadrature formula $$\int\limits_{-\infty}^\infty e^{-z^2}f(z)\,\text dz\approx\sum\limits_{i=1}^{n} w_i f_(z_i),\tag4$$ where $\,z_i\,$ are the roots of the Hermit's polynomial $H_n(z),$ which should provide more than $\,50\,$ correct digits for $\,n=30- 50.\,$

The alternative way is the substitution $$\;t=\operatorname{arccosh}\dfrac1{z},\quad z=\dfrac1{\cosh t},\tag5$$ which transforms the integral $(2)$ into the singular one $$I=\int\limits_0^1 \dfrac{\text dz}{\left(e{\large\mathstrut^{\frac{1+i}{2z}}}-1\right)z\sqrt{1-z^2}}.\tag6$$ However, using the Chebyshev's quadrature in the form $$\int\limits_0^1\dfrac{f(z)\,\text dz}{\sqrt{z(1-z)}} =\dfrac\pi n\sum\limits_{j=0}^n f\left(\cos^2\dfrac{2j-1}{2n}\,\pi\right)\tag7$$ gives $\,49\,$ correct digits for $\,n=1800.\,$