This question will be very similar to:
and
On $$\mathrm{\sum_{x\in\Bbb Z}sech(x), \sum_{x=1}^\infty csch(x)}$$
all of which had closed forms, but it will use this Airy Ai function definition which is a type of Bessel function.
Note that I will actually focus on 2 constants which each converge slowly. I will use $\sum\limits_{n=a}^b A_n=\sum\limits_a^b A_n$ for shorthand and use the following notations. The reason these are split up is because one of the constants may possibly diverge. Note that $\mathrm A_{0,1}$ both have a lower bound of $0$, so the x=$0$ term will be subtracted:
$$\mathrm{A_0=\sum_{-\infty}^0 Ai(x), A_1=\sum_0^\infty Ai(x),A=A_0+A_1-Ai(0)=\sum_{-\infty}^\infty Ai(x)}$$
Here is a graph of the summand:
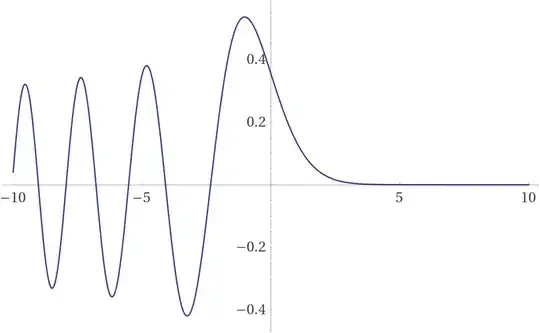
Here is a possible Abel-Plana formula computation.
$$\mathrm{A_0=\sum_0^{\infty}Ai(-x)\mathop=^{Abel}_{Plana}\frac12 Ai(-0)+\int_0^\infty Ai(-x) \,dx+\int_0^\infty\frac{Ai(- -ix)-Ai(- ix)}{e^{2\pi x}-1}\,dx=\frac{1}{3^\frac23 2Γ\left(\frac23\right)}+\frac23+ \int_0^\infty\frac{Ai(ix)-Ai(- ix)}{e^{2\pi x}-1}\,dx}$$
$$\mathrm{A_1=\sum_0^\infty Ai(x)= \mathop=^{Abel}_{Plana}\frac12 Ai(0)+\int_0^\infty Ai(x) \,dx+\int_0^\infty\frac{Ai(-ix)-Ai( ix)}{e^{2\pi x}-1}\,dx= \frac{1}{3^\frac23 2Γ\left(\frac23\right)}+\frac13+ \int_0^\infty\frac{Ai(-ix)-Ai( ix)}{e^{2\pi x}-1}\,dx}$$
This means that the conjectured answer is:
$$\mathrm{A=\sum_{x\in\Bbb Z}Ai(x)=A_0+A_1-Ai(0) \mathop=^{Abel}_{Plana} \frac{1}{3^\frac23 2Γ\left(\frac23\right)}+\frac23+ \int_0^\infty\frac{Ai(ix)-Ai(- ix)}{e^{2\pi x}-1} \, dx + \frac{1}{3^\frac23 2Γ\left(\frac23\right)}+\frac13+ \int_0^\infty\frac{Ai(-ix)-Ai( ix)}{e^{2\pi x}-1}\,dx-Ai(0)= \frac{1}{3^\frac23 Γ\left(\frac23\right)}+ 1+\int_0^\infty\frac{Ai(ix)-Ai( -ix)+Ai(-ix)-Ai(-ix)}{e^{2\pi x}-1}\,dx-\frac{1}{3^\frac23 Γ\left(\frac23\right)}}=1 $$
My final conjecture is the following with alternate forms. Note that some simplifications are possible, but change the definition. The following also uses Hypergeometric functions:
$$\mathrm{1\mathop=^?A=\sum_{-\infty}^\infty Ai(x)=\sum_{x\in\Bbb Z}Ai(x)= \sum_{-\infty}^\infty \left(\frac{\,_0F_1\left(\frac23,\frac{x^3}{9}\right)}{3^\frac23Γ\left(\frac23\right)}-\frac{\,_0F_1\left(\frac43,\frac{x^3}{9}\right)}{\sqrt[3]3 Γ\left(\frac13\right)}\right)} =\sum_{-\infty}^\infty\left(\left(x^\frac32\right)^\frac13I_{-\frac13}\left(\frac{2x^\frac32}{3}\right)-x \left(x^\frac32\right)^{-\frac13} I_\frac13\left(\frac{2x^\frac32}{3}\right)\right) $$
There are also variations with the Airy Bi function, and the Scorer functions Gi and Hi. Please correct me and give me feedback!