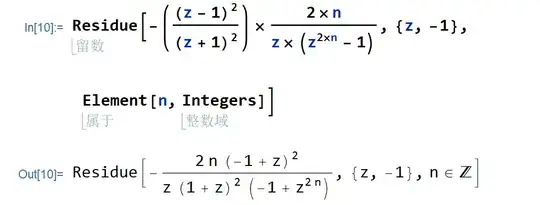While looking at this post (The second answer), I find that it is to tedious to calculate the Residue of
$$ f(z)=-\left(\frac{z-1}{z+1}\right)^2\frac{2n/z}{z^{2n}-1} $$ at $-1$. I do know that we can do this: $$\operatorname*{Res}_{z=-1}f(z)=\frac{1}{2!}\frac{d^2}{dz^2}(f(z)\cdot(z+1)^3).$$ But I am not satisfied with this method. I have the following questions:
1. How many methods do we have to calculate this, can you provide me with an ingenious one?
2. I tried to calculate this via Mathematica like this:[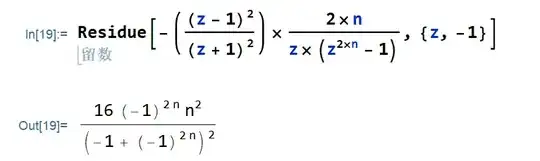 ]
]
If I let $n$ take concrete integers, say, $n=5$, we do get the right answer $-34$. However, it seems that we cann't get the right answer if we let $n$ be a variable. What's wrong here, how can we use mathematica to get a general answer (instead of concrete examples by letting n be some integers). I faced with this sort of problems in similar situations. Can you tell me what shoud I do, or just let me know that mathematica cannot do this! Thank you !
Addition As for Sangchul Lee's answer for my second question, I have another quesion. Why does the following code does not work, what's the difference between "Element[n, Integers]" and "Assumptions -> n \in Integers":