Wolfram and Matlab show different Fourier Transforms for the function $H(z)=\sqrt{\frac{2}{\pi z}}e^{i\left(z-\frac{\pi}{4}\right)}$

Question

I'm struggling with a discrepancy that Wolfram and Maple are giving me. To make everything comprehensible, I describe in the following what I did step by step.

When I let Wolfram calculate the Fourier Transform of the function:

$$H(z)=\sqrt{\frac{2}{\pi z}}e^{i \left(z-\frac{\pi}{4}\right)}$$

by using H[z_]:=Sqrt[2/(Pi*z)]*E^(I(z-Pi/4)); FourierTransform[H[z],z,w], I obtain:

$$ \frac{(1+i) e^{-\frac{1}{4} (i \pi )} (\text{sgn}(w+1)+1)}{\sqrt{2 \pi } \sqrt{\left| w+1\right| }} $$

But when I use Matlab with the following code:

syms x v A w;
% We make the following substitutions:
% A=sqrt(2/pi) and
f = A/sqrt(x) * exp(i*(x-pi/4));
f_FT = fourier(f)

then Matlab yields f_FT=(2^(1/2)*(-1i)^(1/2)*A*pi^(1/2)*(sign(w-1)+1)*(1/2-1i/2))/abs(w-1)^(1/2) which after resubstitution of my variable $A$ leads to:

$$ \frac{2\sqrt{-i}\cdot(\text{sgn}(w+1)+1)\cdot\left(\frac{1}{2}-\frac{i}{2}\right)}{\sqrt{\left| w+1\right| }} $$

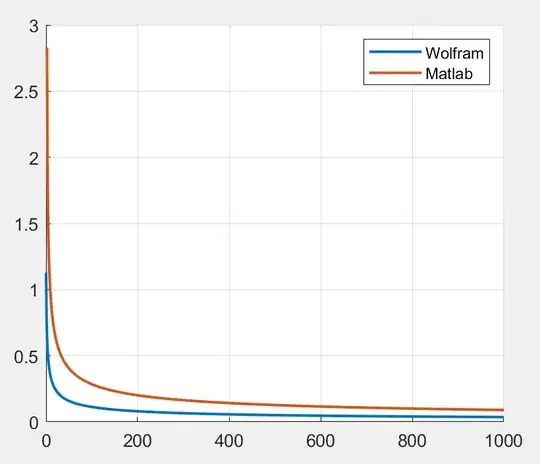
Plotting both results using

w = 0:1:1000;
H1 = ((1+i)*exp(-i*pi/4).*(sign(w+1)+1))./(sqrt(2*pi).*sqrt(abs(w+1)));
H2 = (2*sqrt(-i).*(sign(w-1)+1)).*(1/2-i/2)./(sqrt(abs(w-1)));
figure; hold on;
plot(w, abs(H1), 'LineWidth', 1.5);
plot(w, abs(H2), 'LineWidth', 1.5);
xlim([0 1000])
ylim([0 3])
legend('Wolfram', 'Matlab'); grid on;

lead to the following chart:

Why we have such a kind of discrepancy?

Remark (inspired by Steven Clark):

Dividing the result that I obtained from Matlab by $\sqrt{2\pi}$ and when I accordingly define H2 = (2*sqrt(-i).*(sign(w-1)+1)).*(1/2-i/2)./(sqrt(2*pi).*sqrt(abs(w-1))), then both charts are graphically identical:

Answer 1

Knowing the linearity of Fourier Transform, it's better to remove at first the non-essential factor $\sqrt{\frac{2}{\pi}}e^{-i \pi/4}$ which obscures the global computation.

The proportionnality of the two Fourier transforms, due to different definitions has been thoroughly analysed by @Steven Clark.

I would like to show here that this issue can be followed by referring to known properties of Fourier Transform (that can be found in Tables), meaning in fact that one can bypass the use of software.

In the following, I will not be fully rigorous because I want only to convey the main ideas.

What is the core of the question ? Obtaining the Fourier Transform of $\frac{1}{\sqrt{t}}$ multiplied by $e^{-i(\color{red}{-1})t}$ This kind of multiplication gives rise, in the (frequency) $w$ domain to a shift by $\color{red}{-1}$. As the F. T. of $\frac{1}{\sqrt{t}}$ is $\frac{1}{\sqrt{w}}$ (up to a multiplicative factor, see here with an interesting connection with Fresnel integral) it's not surprising to find $\frac{1}{\sqrt{w}}$ shifted by $\color{red}{-1}$, i.e., $\frac{1}{\sqrt{w-(\color{red}{-1})}}$.

Now, how can be explained the presence of the numerator $sign(w+1)+1$ (which, in particular is $0$ for $w<-1$) ? It is a "testimony" of the fact that this Fourier transform is valid for a certain domain of the variable ; in fact, this Fourier transform should be considered

• with $|t|$ instead of $t$.

• in the sense of distributions. Have you heard about this ?

Answer 2

Another answer has been posted which provides some valuable theoretical insight, but this answer more specifically addresses the actual question.

---

The relationship $\sqrt{\frac{2}{\pi\ z}}=\sqrt{\frac{2}{\pi}}\frac{1}{\sqrt{z}}$ is only valid for $\Re(z)>0$. The correct relationship is $\sqrt{\frac{2}{\pi\ z}}=\sqrt{\frac{2}{\pi}}\sqrt{\frac{1}{z}}$ which for $z<0$ is equivalent to $\sqrt{\frac{2}{\pi\ z}}=-\sqrt{\frac{2}{\pi}}\frac{1}{\sqrt{z}}$.

---

Therefore there appears to be a problem in the assumptions for the Matlab evaluation of the Fourier transform of $H(z)=\sqrt{\frac{2}{\pi z}}e^{i \left(z-\frac{\pi}{4}\right)}$.

---

Using the same false assumption Mathematica evaluates the following statement as True where $H2(\omega)$ is the result of the Matlab Fourier transform evaluation as defined in the question above. The selection of Fourier parameters is described further below.

---

$\text{Assuming}\left[\omega \in \mathbb{R},\text{FullSimplify}\left[\sqrt{\frac{2}{\pi }} \text{FourierTransform}\left[\frac{e^{i \left(z-\frac{\pi }{4}\right)}}{\sqrt{z}},z,\omega ,\text{FourierParameters}\to \{1,-1\}\right]=\text{H2}(\omega )\right]\right]$

---

Mathematica defines the Fourier transform as illustrated in formula (1) below (see Details and Options at Wolfram FourierTransform) where the default Fourier parameters $\{a,b\}=\{0,1\}$ result in Formula (2) below and the Fourier parameters $\{a,b\}=\{1,-1\}$ result in Formula (3) below.

---

$$\mathcal{F}_x[f(x)](\omega)=\sqrt{\frac{| b| }{(2 \pi )^{1-a}}} \int\limits_{-\infty }^{\infty } f(x) e^{i b x \omega } \, dx\tag{1}$$

$$\mathcal{F}_x[f(x)](\omega )=\sqrt{\frac{1}{2 \pi }} \int\limits_{-\infty }^{\infty } f(x) e^{i x \omega } \, dx\ ,\quad\{a,b\}=\{0,1\}\tag{2}$$

$$\mathcal{F}_x[f(x)](\omega )=\int\limits_{-\infty }^{\infty } f(x) e^{-i x \omega } \, dx\ ,\quad\{a,b\}=\{1,-1\}\tag{3}$$

---

Matlab defines the Fourier transform as follows (see Matlab Fourier Transform) where the $fourier$ function uses the parameters $\{c,s\}=\{1,-1\}$.

---

$$\mathcal{F}_x[f(x)](\omega)=c \int\limits_{-\infty}^{\infty} f(x) e^{i s x \omega } \, dx\tag{4}$$

---

Therefore using the Fourier parameters $\{a,b\}=\{1,-1\}$ in Mathematica is equivalent to using the Fourier parameters $\{c,s\}=\{1,-1\}$ in Matlab.