Fourier Transform of 2D Free-Space Green's Function (Hankel Function)

Question

I read in a book chapter by U. Frisch (Wave Propagation in Random Media) which states the 3D free space Green's function in the spatial domain as:

$$G(r,r')=\frac{\exp\big(ik(r-r')\big)}{-4\pi(r-r')}$$ And in the frequency domain (after Fourier Transform) as:

$$G(k)=({k_0}^2-k^2)^{-1}$$ I am trying to do the same operation with the 2D Green's Function which contains a Hankel operator to obtain a formulation in the frequency domain:

$$G_{2\mathrm D}(r)=\frac{i}{4}H_{0}^{(1)}(k_0r)$$ Something I have tried is to obtain a simplified formulation of the Green's function from https://dlmf.nist.gov/10.2 (equation 10.2.5):

$$H^{(1)}_{\nu}(z)\sim\sqrt{2/(\pi z)}~\mathrm{e}^{\mathrm i\left(z-\frac{1}{2}\nu \pi-\frac{1}{4}\pi\right)}$$ Then, I tried doing the Fourier transform operation for this simplified Hankel function, but to no avail as integration by parts does not converge to a solution due to the sqrt(1/z) term.

Does anyone have any suggestions on how I can Fourier Transform the 2D Green's function? Thank you.

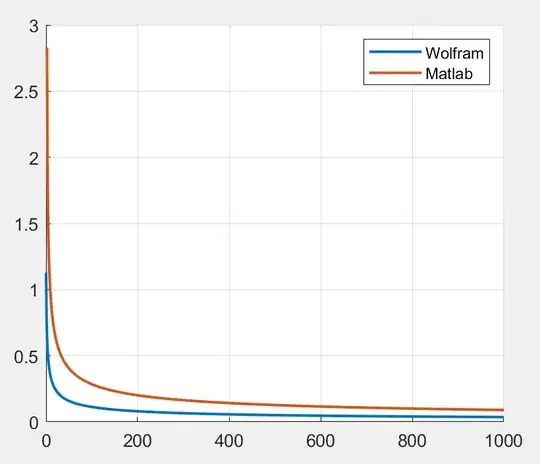
EDIT: Eldar has suggested the use of a computational approach to obtain the result. We observe a discrepancy when using MATLAB and Wolfram to do the analysis and that is most likely due to the convention used between the 2 softwares in the Fourier Transform operation.

Answer 1

When I try to make a Fourir Transform (with respect to $z$) of your simplified function:

$$H(v,z)=\sqrt{\frac{2}{\pi z}} e^{i \left(-\frac{\pi v}{2}+z-\frac{\pi }{4}\right)}$$

then by a computational approach using H[v_,z_]:=Sqrt[2/(Pi*z)]*E^(I(z-v*Pi/2-Pi/4)); FourierTransform[H[v,z],z,w], I obtain:

$$\frac{(1+i) e^{i \left(-\frac{\pi v}{2}-\frac{\pi }{4}\right)} (\text{sgn}(\omega +1)+1)}{\sqrt{2 \pi } \sqrt{\left| \omega +1\right| }}$$

The transformation (with frequency variable $\omega$) includes the following sum of both, the cosine transform for the even and the sine transform for the odd part:

$$ \large\begin{array}{l} F_x\left(\sqrt{\frac{2}{\pi x}}e^{i\left(-\frac{\pi v}{2}+x-\frac{\pi}{4}\right)}\right)(\omega)=\\ F_x^c\left(-\frac{(-1)^{\frac{3}{4}} \left(\sqrt{-\frac{1}{x}}+e^{2ix}\sqrt{\frac{1}{x}}\right)}{\sqrt{2 \pi}e^{\frac{1}{2}i(\pi v+2x)}}\right)(\omega)+i\cdot F_x^s\left(\frac{(-1)^{\frac{3}{4}}\left(\sqrt{-\frac{1}{x}}-e^{2ix}\sqrt{\frac{1}{x}}\right)}{\sqrt{2\pi}e^{\frac{1}{2}i(\pi v+2x)}}\right)(\omega) \end{array} $$

The Fourier cosine transform for the even part is:

$$ \large\begin{array}{l} \sqrt\frac{2}{\pi}\int_{0}^{\infty}-\frac{(-1)^{\frac{3}{4}}e^{-\frac{1}{2}i(\pi v+2x)}\left(\sqrt{-\frac{1}{x}}+e^{2ix}\sqrt{\frac{1}{x}}\right)\cos(\omega x)}{\sqrt{2\pi}}\,dx=\\ \frac{\left(-\frac{1}{2}-\frac{i}{2}\right)(-1)^{\frac{3}{4}}\left(\sqrt{\left|1-\omega\right|} (\text{sgn}(\omega +1)+1)+\sqrt{\left| \omega +1\right|}(\text{sgn}(1-\omega )+1)\right)}{\sqrt{2\pi }e^{\frac{i\pi v}{2}} \sqrt{\left|1-\omega\right|}\sqrt{\left|\omega+1\right|}} \end{array} $$

The Fourier sine transform for the odd part is:

$$ \large\begin{array}{l} \sqrt\frac{2}{\pi}\int_{0}^{\infty}\frac{(-1)^{\frac{3}{4}}e^{-\frac{1}{2}i(\pi v+2x)}\left(\sqrt{-\frac{1}{x}}-e^{2ix}\sqrt{\frac{1}{x}}\right)\sin(\omega x)}{\sqrt{2\pi}}\,dx=\\ \frac{\left(-\frac{1}{2}+\frac{i}{2}\right) (-1)^{\frac{3}{4}} \left(\sqrt{\left|1-\omega \right|}(\text{sgn}(\omega+1)+1)-\sqrt{\left|\omega+1\right|} (\text{sgn}(1-\omega)+1)\right)}{\sqrt{2\pi}e^{\frac{i\pi v}{2}} \sqrt{\left|1-\omega\right|}\sqrt{\left|\omega+1\right|}} \end{array} $$

Answer 2

One additional finding in order to make my first answer plausible using Matlab.

When using Matlab and perform the following simplifying substitution $A=\sqrt{\frac{2}{\pi}}$, then with the following code:

syms x A;
% We make the following substitutions:
% A=sqrt(2/pi) and
f = A/sqrt(x)exp(i(x-pi/4));
f_FT = fourier(f)

we obtain the solution:

f_FT=(2^(1/2)*(-1i)^(1/2)*A*pi^(1/2)*(sign(w-1)+1)*(1/2-1i/2))/abs(w-1)^(1/2)

which differs to Wolfram's solution as shown by the following graphs:

This discrepancy opens a new issue (to be investigated).

Remark 1

When I divide the result obtained by Matlab by $\sqrt{2\pi}$ and accordingly define H2 = (2*sqrt(-i).*(sign(w-1)+1)).*(1/2-i/2)./(sqrt(2*pi).*sqrt(abs(w-1))), then both charts are graphically identical:

Remark 2

When using the following two substitutions:

• $A=\sqrt{\frac{2}{\pi}}$
• $B=\frac{\pi}{4}$

and running the code:

syms x A B;
% We make the following substitutions:
% A=sqrt(2/pi) and
f = A/sqrt(x)exp(i(x-B));
f_FT = fourier(f)

Then Matlab yields the result f_FT=((-1i)^(1/2)*A*pi^(1/2)*exp(-B*1i)*(sign(w-1)+1))/abs(w-1)^(1/2)