1

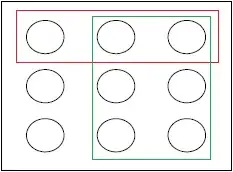
Definition of the Pebble World (taken from Stat 110): In the Pebble World, the definition says that probability behaves like mass: the mass of an empty pile of pebbles is $0$, the total mass of all the pebbles is $1$, and if we have non-overlapping piles of pebbles, we can get their combined mass by adding the masses of the individual piles. The pebbles can be of differing masses and we can also have a countably infinite number of pebbles as long as their total mass is $1$.

enter image description here

In the above image, suppose each pebble weighs $\frac{1}{9}$ (for brevity). The pebbles inside the red box denote event $A$ and the pebbles inside the green box denote the event $B$. Note that the two boxes are intersecting.

What is $P(A | B)$? It's supposed to be the probability of $A$ given $B$ has occurred, which means, $\frac{2/9}{6/9} = \frac{1}{3}$. How do we explain this intuitively? ($1/3$ feels like selecting the one element that's not in the intersection upon all the elements inside the red box. I don't think it's meant to be this way.)

dictatemetokcus
  • 585
  • 1
    $P(A,|,B)$ is the probability that a pebble is in $A$, given that it is in $B$. There are exactly $6$ pebbles in $B$, $2$ of which are in $A$. So the answer is $\frac 26=\frac 13$. – lulu Aug 21 '21 at 16:04
  • @lulu So it means, $P(A | B)$ is the probability of drawing a pebble in $A$ such that it is in $B$. This means, $(A | B) \subset B$ right, i.e., $P(A | B) \leq P(B)$? – dictatemetokcus Aug 21 '21 at 16:54
  • Additionally, @lulu, this is where is collected the problem from. It seems there is an error in the article. – dictatemetokcus Aug 21 '21 at 17:03
  • Your inequality is incorrect. Say $A=B$. Then $P(A,|,B)=1$, but $P(B)$ need not be $1$. – lulu Aug 21 '21 at 17:05
  • 1
    Also, your interpretation is incorrect. $P(A,|,B)$ is the probability of drawing a drawing a pebble from $A$ given that you are only drawing from pebbles in $B$. Don't confuse $P(A,|,B)$ with $P(A\cap B)$. – lulu Aug 21 '21 at 17:07
  • @lulu Just to be clear, does $P(A \cap B)$ mean the probability of a pebble being in $A$ such that it is also in $B$? (In other words, it's the probability of drawing a pebble that is simultaneously in $A$ and $B$.) It is $2/9$ in this case. – dictatemetokcus Aug 21 '21 at 17:33
  • Yes. The intersection of two events refers to the event that both occur. – lulu Aug 21 '21 at 17:35
  • @lulu I think I said exactly what you wrote for $P(A | B)$, maybe my wording isn't proper? I meant, probability of drawing a pebble in $A$ such that it is in $B$. This means, you will have to select a pebble from $A$ such that it already is in $B$. Is it correct now? (Sorry for repeating the same question.) – dictatemetokcus Aug 21 '21 at 17:37
  • Once again, the conditional probability is NOT the same as the probability of the intersection. – lulu Aug 21 '21 at 17:58
  • 1
    You might find this answer, which I just wrote, helpful on how to think about/visualise/intuit/understand the concept of independence of events. – ryang Aug 21 '21 at 18:12
  • @lulu Yes, so in the intersection, the pebble will have to be in both $A$ and $B$ out of a total $|S|$ pebbles, while in the case of conditional probability (and in particular, $A|B$), the pebble has to be selected from the intersection out of a total of $|B|$ pebbles. – dictatemetokcus Aug 21 '21 at 23:50
  • No. In the intersection, the pebble is drawn from the whole population and must be in both $A,B$. In the conditional event, the pebble is drawn from $B$ and must then also be in both. In the first you are drawing from (potentially) a much larger sample. – lulu Aug 21 '21 at 23:53
  • @lulu $S$ denotes the whole population. It's the sample space. The whole population is of size $|S|$ and the population in $B$ is $|B|$. – dictatemetokcus Aug 21 '21 at 23:58
  • What you wrote was very vague. You wrote "selected from the intersection" but you are selecting from $B$. If you are trying to get the definitions right, be precise. – lulu Aug 22 '21 at 00:00
  • Above you wrote "This means, $(A|B)\subset B$, right?". This shows an important confusion. There is no set "$A|B$". The notation is confusing! - but $P(A|B)$ does not denote the probability of some set called $A|B$. Rather $P(A|B)$ is defined to mean $P(A\cap B)/P(B)$. $A\cap B$ and $B$ denote sets, but $A|B$ does not. Quite possibly, there is no actual set in your probability space with probability $P(A|B)$. (For example in your pebble model above with $9$ pebbles with equal mass $1/9$, you can find $A$ and $B$ with $P(A|B)=1/2$, but there is no set $C$ in your model with $P(C)=1/2$.) – James Martin Aug 22 '21 at 09:27
  • @lulu Can we say it in this manner then: $P(A|B)$ is the probability that $A$ occurs given $B$ is the sample space? (I know there's no need to use these definitions, I am trying to check if this statement is equivalent.) – dictatemetokcus Aug 22 '21 at 20:28
  • @JamesMartin I realized that, it doesn't mean anything. And thank you! – dictatemetokcus Aug 22 '21 at 20:29
  • 1
    @dictatemetokcus That's much better. In more general contexts, you'd want to say what distribution you are using on $B$. Here, it is clear that we are just using counting measure. The computational definition, $P(A,|,B)=\frac {P(A\cap B)}{P(B)}$, avoids this as you are only working with the probability distribution on the full sample space. – lulu Aug 22 '21 at 20:34
  • @lulu This resolves all my questions. Thank you once again. – dictatemetokcus Aug 22 '21 at 20:37

1 Answers1

1

Let:

  • the sample space (picking any pebble) be the black square;
  • $A$ be event of picking any pebble within the red rectangle;
  • $B$ be event of picking any pebble within the green rectangle.

Say, we know that event $B$ occurs; this means that $A$ can possibly eventuate from within the green rectangle. In other words, being given that $B$ occurs is the same as narrowing down the effective sample space from the black square to the green rectangle.

In this case (i.e., given that $B$ occurs) the probability of $A$ $$=\frac{\text n(\text{‘success’})}{\text n(\text{the effective sample space})}\\=\frac{\text n(\text{the part of the red rectangle that's inside the green rectangle})}{\text n(\text{the green rectangle})}\\=\frac{\text n(A\cap B)}{\text n(B)}.$$

In other words, $$P(A|B)=\frac{\text n(A\cap B)}{\text n(B)}\\=\frac26\\=\frac13.$$

ryang
  • 38,879
  • 14
  • 81
  • 179
  • This is helpful, thank you so much. When two events are independent, we write it as $P(AB) = P(A)P(B)$ but this doesn't make any sense to me (intuitively). When we write it as $P(A|B) = P(A)$, it makes sense why the events are independent as it corresponds to: the occurrence of $A$ remains unchanged despite the occurrence of $B$. But the multiplication does not mean anything like that.. just from the equation. So could you please give me an intuitive explanation of that? – dictatemetokcus Aug 22 '21 at 20:50
  • The former equality, which defines independence of two events, is actually motivated by the latter equality, which results from our informal/intuitive characterisation of the concept. The definition is more general, since it allows both $A$ and $B$ to have probabilities $0.$ You might find these $,$ two other answers that I wrote helpful in further thinking about and understanding the concept. – ryang Aug 22 '21 at 20:58
  • Oooh so the former inequality is motivated by the latter one. Then it makes sense. For $n$ events, we can similarly write $P(A_i | A_{j_1} \cap \cdots A_{j_{r}}) = P(A_i)$ (where $r < n$, $A_{j_k} \neq A_i$ and ${j_1, \cdots, j_r} \subset {1, 2, \cdots, n}$) to define independent events and eventually write in the product form. – dictatemetokcus Aug 22 '21 at 21:43
  • Yes, that works (though I've only seen the direct generalisation from the 2-event formal defn.) Re: the informal characterisation: there are actually two slightly different versions: $P(A|B)=P(A|B^c)$ versus $P(A|B)=P(A).$ Both lead to $P(A\cap B)=P(A)P(B);$ however, the former has a tighter restriction than the latter. – ryang Aug 22 '21 at 22:11
  • $P(A | B^C) = \frac{P(A \cap B^C)}{P(B^C)}$ which equals $P(A)$ iff $A$ and $B^C$ are independent events. But that is not necessarily true. So how does the first variation lead to $P(A \cap B) = P(A)P(B)$ (since the two do not seem to be equivalent definitions)? – dictatemetokcus Aug 22 '21 at 22:36
  • Done. Here's the link – dictatemetokcus Aug 23 '21 at 21:14