This question takes inspiration from
and other fractal questions.
Let me introduce the Darboux function which has fractal properties due to being a continuos nowhere differentiable function. Here is the definition. Do not confuse the Darboux function with similar names.
$$\mathrm{Darboux(x)=D(x)=\sum_{n=1}^\infty \frac{sin((n+1)!x)}{n!}}$$
Here is the integral to be solved:
$$\mathrm{\int_0^1 D(x) dx=\int_0^1 \sum_{n=1}^\infty \frac{sin((n+1)!x)}{n!} dx= -\sum_{n=1}^\infty \frac{cos((n+1)!x)}{n!(n+1)!}\bigg|_0^1= -\sum_{n=1}^\infty \frac{cos((n+1)!x)}{(n+1)n!^2}\bigg|_0^1=\sum_{n=1}^\infty \frac{1}{(n+1)!n!}-\sum_{n=1}^\infty \frac{cos((n+1)!)}{n!(n+1)!}= \sum_{n=1}^\infty \frac{1-cos((n+1)!)}{(n+1)n!^2}}$$
The evaluation at 0 term will remind you of a Bessel function because of the factorial term squared in the denominator. So far our partial final answer is:
$$\mathrm{\int_0^1 D(x)dx=I_1(2)-1-\sum_{n=1}^\infty \frac{cos((n+1)!)}{(n+1)n!^2}= I_1(2)-1-\sum_{n=1}^\infty \frac{cos((n+1)!)}{n!(n+1)!}= I_1(2)-1-\sum_{n=2}^\infty \frac{cos(n!)}{Г(x)n!}= I_1(2)-1-\sum_{n=2}^\infty \frac{cos(n!)}{nΓ^2(n)}= I_1(2)-1- Re\sum_{n=2}^\infty \frac{e^ {i\,n!}}{nΓ^2(n)}= I_1(2)-1- Re\sum_{n=2}^\infty \frac{e^ {i\,n!}}{Γ(n)n!}= .71547…}$$
Finally, here is an interactive graph of the Darboux function and a beautiful visual representation of the constant: 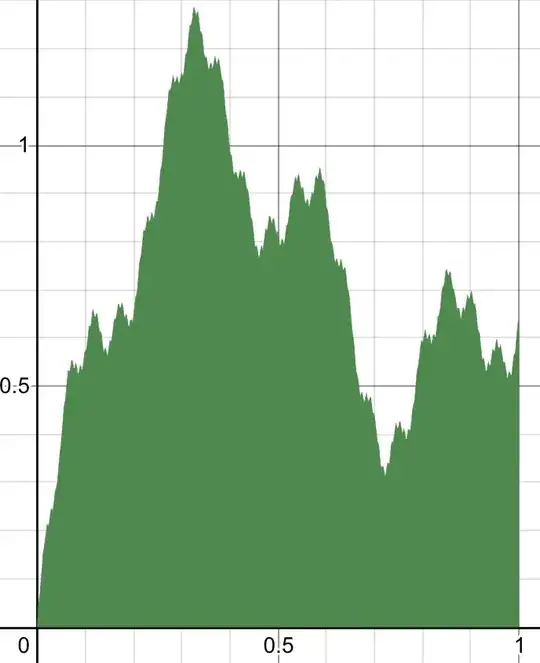
Here is a possible way to see a connection between the results:
$$\mathrm{D(1)=Im\sum_1^\infty\frac{e^{i (n+1)!}}{n!}}$$
while our goal integral and sum is:
$$\mathrm{\int_0^1 D(x) dx=I_2(1)-1-Re\sum_2^\infty\frac{ne^{i n!}}{n!^2}}$$
How do I evaluate the aforementioned cosine and factorial series? It seems to part of a more general Darboux function, but I cannot find much on it. I already have sum and integral representations, so now I need a better form as a closed form seems impossible using known functions. If there is a closed form, then it may be in terms of the D(x) Darboux function. A better form is one that written in exact form and possibly uses new functions, but it equal to our goal problem. Please correct me and give me feedback!