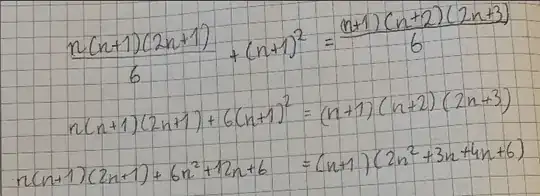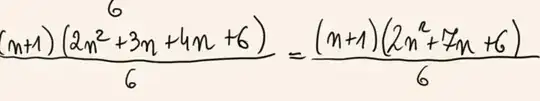0

I am trying to solve this question. I have to proove that L = R side Question:

$1^2+2^2+\ldots+n^2=\frac{n(n+1)(2n+1)}6$

What I got so far, I am stuck on third step, the numbers seem too big. I do not know what I'm doing wrong. Can someone assist me please? enter image description here

This is the expected answer enter image description here

etoRatio
  • 247
  • 2
    This question has been asked before. Here's just one of them: https://math.stackexchange.com/questions/2824803/sum-of-the-square-of-natural-numbers-mathematical-proof – RobertTheTutor Jul 23 '21 at 20:26
  • Welcome to Mathematics Stack Exchange. Divide both sides by $n+1$ if you like smaller numbers – J. W. Tanner Jul 23 '21 at 20:28
  • Hint: don't expand the r.h.s. Factor $n+1$ in the l.h.s. instead, and factorise the quadratic polynomial that is the other factor. – Bernard Jul 23 '21 at 20:29
  • I've added the expected answer, I got the right side done, I just have trouble with the left side. The thing with 6(n+1)^2 doesn't seem right to me. – etoRatio Jul 23 '21 at 20:36

2 Answers2

4

I wouldn't solve it the way you have done since you've equated the expressions without establishing that they are equal. Instead, you should take one side and manipulate it to achieve the other side. For example, you can take the left side and do the following:

$$\begin{eqnarray} \frac{n(n+1)(2n+1)}{6} + (n+1)^2 &= \frac{n(n+1)(2n+1)+6(n+1)^2}{6} \\ &=\frac{(n+1)(n(2n+1)+6(n+1))}{6} \\ &=\frac{(n+1)(2n^2+n+6n+6)}{6} \\ &=\frac{(n+1)(2n^2+7n+6)}{6} \\ &=\frac{(n+1)(n+2)(2n+3)}{6} \\ \end{eqnarray} $$

Kman3
  • 2,479
2

The thing with $6(n+1)^2$ in the LHS of your second line is fine. Continue by factoring out the $n+1$ from the LHS. You get $$n(n+1)(2n+1)+6(n+1)^2=(n+1){\big[} n(2n+1) + 6(n+1){\big]}=(n+1)(2n^2+n+6n+6) $$ Next, divide through by $6$ and you will agree with the expected LHS.

You can also reach the expected LHS from your third line. First factor $6n^2+12n+6$ into $(n+1)(6n+6)$. The LHS of your third line is then $$\begin{aligned} n(n+1)(2n+1)+6n^2+12n+6&=n(n+1)(2n+1)+(n+1)(6n+6)\\ &=(n+1)\big[n(2n+1)+(6n+6)\big]\\ &=(n+1)(2n^2+n+6n+6) \end{aligned} $$

grand_chat
  • 38,951