1

According to Approach0, this is new to MSE.

In classical logic, there is the notion of antecedent strengthening; namely:

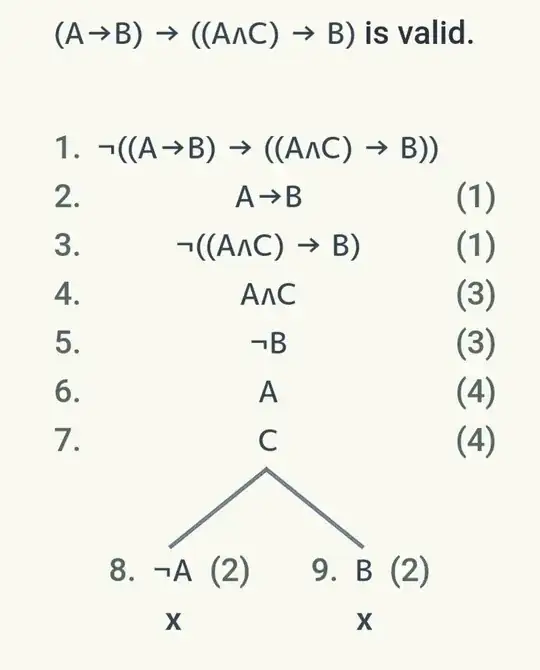
$$(A\to B)\to((A\land C)\to B)$$

is valid. A proof via tableau is given below.

enter image description here

It was generated here.

However, in a document on nonclassical logic (which can be found here), the following "counterexample" is given:

If Romney wins the election, he'll be sworn in in January. Therefore, if Romney wins the election and dies of a heart attack the same night, he'll be sworn in in January.

Here $A$ is "Romney wins the election", $B$ is "Romney will be sworn in in January", and $C$ is "Romney dies of a heart attack the same night as he wins the election".

My question is:

How does classical logic handle this supposed counterexample? What, if anything, is wrong with it?

I have a longstanding interest in nonclassical logics. See here for instance.

I doubt I could answer this myself. I don't want to end up a crank or anything, so I'm looking for an answer with full proofs or at least references.

I hope I have provided enough context.

Please help :)

Shaun
  • 44,997
  • 8
    One could say that the premise "If Romney wins the election, he'll be sworn in in January" is simply false because it is imprecise, since strictly speaking what is meant is "If Romney wins the election, then if all goes well and nothing unexpected intervenes, he'll be sworn in in January", in which case the conclusion no longer follow. – Natalie Clarius Jun 27 '21 at 20:00
  • 3
    In order for the hypothesis "If Romney wins the election, he'll be sworn in in January" to be true (and dead people can't be sworn in), it must not be possible for Romney to die of a heart attack the same night. The only way this is problematic is if we can simultaneously accept "If Romney wins the election he'll be sworn in in January" and "Romney could die of a heart attack the night of the election" as true. The only issue is whether we interpret "If A then B" in its strict sense or as "If A then B unless something surprising happens." – Noah Schweber Jun 27 '21 at 20:02
  • The context of the quote in the paper you link had a potentially-key piece of context you did not mention, which is that the author believes that "Conditional Logic" is a solution to the problem of that example. At a quick skim, it seems the suggestion is to formalize it as something like "In possible worlds close to our own (where Romney does not die of a heart attack the night of the election), we had 'if Romney wins the election he'll be sworn in in January'". At least some details of the formal setup for "possible worlds close to our own" is in the paper you quoted. – Mark S. Jun 27 '21 at 20:15
  • The relation is only valid if A strictly implies B. Statement C is then redundant. For example: A = {Today is a monday.} B = {Tomorrow is a tuesday.} C = {It is raining today.}. You can also take C = {Yesterday was a sunday.}. This strengthens statement A, but adds nothing new to the relation between A and B. – M. Wind Jun 27 '21 at 22:25
  • It is the well-known counter-intuitive aspect" of truth-functional conditional connective (in Classical logic): it is "timeless" and "a-causal". Thus, if it it true that "If Romney wins the election, he'll be sworn in in January", it means that the possibility that "Romney wins the election" is TRUE and "Romney, will be sworn in in January" is FALSE is ruled-out. 1/2 – Mauro ALLEGRANZA Jun 28 '21 at 10:44
  • 2
    If this is not so, because maybe "Romney dies of a heart attack the same night as he wins the election", this means that the row TRUE-FALSE in the truth table for $A \to B$ is a possibility and this means that the conditional $A \to B$ is not TRUE. 2/2 – Mauro ALLEGRANZA Jun 28 '21 at 10:44

1 Answers1

1

You are questioning the validity of $(A\to B)\to((A\land C)\to B)$ when $C$ implicitly contradicts $B$.   Well, let's consider when it explicitly does so; namely when $C$ is $\lnot B$.

For any statement $\varphi$ we consider $\varphi\to(\lnot\varphi\to B)$ to be valid, by way of the Principle of Explosion (aka ex falso quodlibet, EFQ).   When the premises contain a contradiction, then anything may be derived.

$$\begin{split}\varphi\,,\lnot\varphi&\vDash B\\[3ex]\therefore\qquad &\vDash \varphi\to(\lnot\varphi\to B)\end{split}$$

Well, since this holds for any statement $\varphi$, let's consider when $\varphi$ is $(A\to B)$.   Then $\lnot\varphi$ is equivalent to $A\land\lnot B$.   So by substitution we have : $$\vDash (A\to B)\to((A\land\lnot B)\to B)$$

Shaun
  • 44,997
Graham Kemp
  • 129,094