1

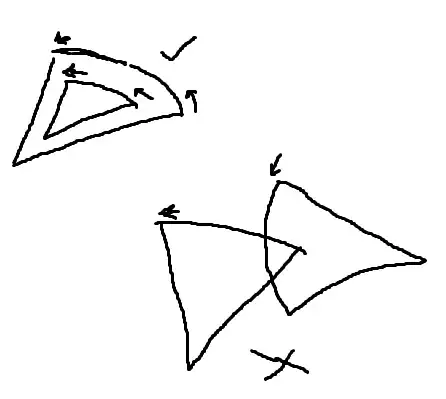
I have two arcs defined with the following information:

Origin, Radius, StartPoint, EndPoint, StartAngle & EndAngle

The angles are signed so you know which direction around the circle the arc goes.

An arc inside an arc segment does not count as an overlap as the perimeters don't touch:

enter image description here

Is it possible to test if the two arcs intersect along their perimeters (I am not looking to test if the area of the circle segments overlap).

My current idea is using an algorithm to interpolate along the arcs as straight line segments and do line-line intersection tests for each line segment - which can be slow depending on how many line segments i use, but I am wondering if there is a more pure mathematical approach ?

WDUK
  • 480
  • There is the minor issue that such information for a single arc does not in itself distinguish between a short arc and a long arc. Are you supposed to take the short arc or the anti-clockwise arc or something else? – Henry Jun 16 '21 at 00:09
  • Find the intersections between the two circles and check if any of them falls within the arcs. – dxiv Jun 16 '21 at 00:11
  • Oh, my bad, let me rephrase it the arcs are defined with a start point and end point so i'll reword it. – WDUK Jun 16 '21 at 00:11
  • @dxiv an arc can fall inside another arc but not intersect at perimeter so it being within an arc doesn't mean it intersects. – WDUK Jun 16 '21 at 00:12
  • 1
    @WDUK Not sure what you mean. Any intersection between the arcs is an intersection between the circles that the arcs belong to. There can only be 0, 1 or 2 such intersections (or infinitely many if the circles coincide). So you can determine those intersections, then check if any of them fall within the arcs. – dxiv Jun 16 '21 at 00:16
  • @dxiv I can test the circles overlap easily but not sure how to then check if just the arc's perimeters overlap each other. Its finding the intersection points that i don't know how to calculate at least mathematically. – WDUK Jun 16 '21 at 00:20
  • @WDUK How can I find the points at which two circles intersect? – dxiv Jun 16 '21 at 00:22

1 Answers1

1

One way to approach is this problem is to think circles rather than arcs:

First check if the two large circles intersect at all. This can be done by comparing the distance between the centers ($d$) with the sum of radii ($r_1 + r_2$). Let's suppose $r_1 \ge r_2$

  1. If $d > r_1 + r_2$ then the circles are outside each other and don't have any intersection points, and therefore neither do the arcs.

  2. If $d = r_1 + r_2$ then the circles are outside each other and touch at one point only, which is on the line connecting their centers.

  3. If $r_1 - r_2 < d < r_1 + r_2$ then the circles meet at two points.

  4. If $d = r_1 - r_2$ then the smaller circle is in the larger circle and touches it at only one point (analysis of the case where the radii are equal and the circles completely overlap is left as an exercise to the interested reader)

  5. If $d < r_1 - r_2$ then the smaller circle is in the larger circle and the two circles don't have any intersection points, therefore neither do the arcs.

Next, find the meeting points (if any) of the circles. This can be done by solving the system of equations of the two circles. This step gives up to 2 points.

Next, for each intersection point identified in the previous step, determine if it lies on the given arcs. This can be done through the following steps for each arc:

  1. Find the angle of that point with respect to the center of the arc.
  2. Compare the angle of the point (computed above) with the start and end angles of the arc. The point is on the given arc if its angle is between the start angle and end angle of the arc.

If the point of intersection of the circles is on both arcs then you have an answer.

Saeed
  • 1,872
  • Do you know of a good source to explain how to find the intersecting points for 2 overlapping circles that you mentioned? My data is not written in a circle equation form so i need to find one that shows it in vector form. – WDUK Jun 19 '21 at 02:27
  • @WDUK Please explain more about your data. Is it two polygons? Why not use equations? If you have the center and radius of a circle, that information is enough to write its equation. If you can use circle equations, then I see that user dxiv has left a link to useful methods. I like the first answer in that link. – Saeed Jun 19 '21 at 03:53
  • @WDUK A different (and maybe naive) approach would be to compare your vector images to raster images and directly check if they have any overlapping pixels! – Saeed Jun 19 '21 at 03:56
  • Strangely I did think about this, not sure how accurate pixel overlaps would be in comparison to a a game world unless i use a really high resolution relative to my max world size. It would be interesting to work out the max resolution for such tests that equate to the same precision you get from floating points. – WDUK Jun 19 '21 at 04:08
  • @WDUK Sorry, typo: "convert your vector images to raster". If you'd like to do this, the overall running time of the program may be reduced by starting image processing at a coarse resolution: if the shapes do not overlap in the coarse resolution then there is no need to construct fine resolution images. – Saeed Jun 19 '21 at 04:19
  • thats a good idea! Do you know any articles that have implemented that idea so i can look into it more? – WDUK Jun 19 '21 at 04:20
  • 1
    @WDUK Sorry I don't have a specific reference in mind. A general reference for processing vector images is the book 'Computational Geometry' by de Berg et al (doi 10.1007/978-3-540-77974-2). I'm not sure if it helps with this question in particular, but hope you find the book useful. – Saeed Jun 19 '21 at 04:39
  • 1
    Thanks for the help :) – WDUK Jun 19 '21 at 04:42