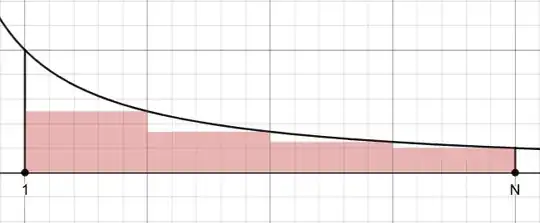
Let $N\geqslant1$ be an integer. Then which of the following statements are true ?
$\displaystyle\sum\limits_{n=1}^N\dfrac1n\leqslant1+\log N$
$\displaystyle\sum\limits_{n=1}^N\dfrac1n<1+\log N$
$\displaystyle\sum\limits_{n=1}^N\dfrac1n\leqslant\log N$
$\displaystyle\sum\limits_{n=1}^N\dfrac1n\geqslant\log N$
My Attempt : $$\underbrace{\frac11+\frac11+\frac11+\frac11+\frac11+\frac11+\ldots+\frac11}_{N\text{ times}}=N$$
$$\geqslant\sum_{n=1}^N\frac1n=\frac11+\frac12+\frac13+\frac14+\frac15+\frac16+\ldots+\frac1N$$
$$\geqslant\underbrace{\frac1N+\frac1N+\frac1N+\frac1N+\frac1N+\frac1N+\ldots+\frac1N}_{N\text{ times}}$$
$$=\frac NN=1$$
$$\implies1\leqslant\sum_{n=1}^N\frac1n\leqslant N$$
Also $\;\log N\leqslant N,\;\forall N\geqslant1\,.\;$ I'm unable to combine this information to answer the question. Please help me.