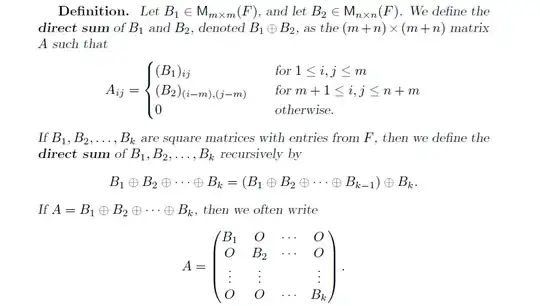Prove that $\det(T) = \det(T_{w_{1}})\det(T_{w_{1}})\cdots \det(T_{w_{k}})$ where $W_{i}$ are $T$-invariant subspaces of $V$ - Trouble at last step.

Question

Let $T$ be a linear operator on a finite dimensional vector space $V$ and let $W_{1} \oplus \cdots \oplus W_{k}$ where $W_{i}$ are $T$-invariant subspaces of $V$. Prove that $\det(T) = \det(T_{w_{1}})\det(T_{w_{1}})\cdots \det(T_{w_{k}})$

Prior to attempting to prove the question I have two relevant pieces of information to use:

Attempt:

Let $\beta_{i}$ be an ordered basis for $W_{i}$ such that $\beta = \cup \beta_{i}$ is a basis for $V$. As such we let $A = [T]_{\beta}$ and $B_{i} = [T_{W_{i}}]_{\beta_{i}}$.

As a result of this $A = B_{1} \oplus B_{2} \cdots \oplus B_{k}$. Observe $A$ is a diagonal matrix. As a result $\det(A)$ is the product of the diagonal.

$$\det(A) = \prod_{i = 1}^{k}B_{i}$$

Here is where I'm having an issue in making the logical jump. What I worked out occurring after working from the other direction would be

$$\text{missing steps} \\ = \prod_{i=1}^{k} \det(B_{i}) \\ = \prod_{i=1}^{k} \det(T_{W_{i}})$$

I know I can take the determinants of the individual $B_{i}$ because they are square matrices, but the determinant is not a linear operator so I can't just do

$$\det( \prod_{i=1}^{k}(B_{i}) = \prod_{i=1}^{k} \det(B_{i})$$

As well it is not the case that $A = \prod_{i=1}^{k}(B_{i}$, only the $\det(A) = \prod_{i=1}^{k}(B_{i})$.

So what is it that I'm missing to get the final result I'm desiring?

Answer 1

Question: "So what is it that I'm missing to get the final result I'm desiring?"

Answer: Here is a proof using the exterior product: If $\phi: V \rightarrow V$ is an endomorphism of a vector space, you may calculate the determinant of the endomorphism $\phi$ as the induced map

$$\wedge^n (\phi): \wedge^n V \rightarrow \wedge^n V$$

where $n:=\dim(V)$. Since $\wedge^n$ is a functor you get a canonical map $\wedge^l (\phi)$ for any integer $l \geq 1$.

It follows $\wedge^n (\phi)$ is an endomorphism of a one dimensional vector space $\wedge^n V$ and hence it is given as multiplication with a number $a$. The number $a$ is the determinant: $a=\det(\phi)$ of the map $\phi$. If you choose a basis $B$ of $V$ and the matrix of $\phi$ in this basis is a matrix $A$, it follows $a=det(A)$ is the determinant of the matrix $A$.

There is a formula:

$$\wedge^{n_1+n_2}(V_1\oplus V_2) \cong \wedge^{n_1}V_1 \otimes \wedge^{n_2}V_2,$$

where $n_i:=\dim(V_i)$. Let

\begin{align*} \phi= \begin{pmatrix} \phi_1 & 0 \\ 0 & \phi_2 \end{pmatrix} \end{align*}

where $\phi_i$ is an endomorphism of $V_i$. It "follows"

$$\det(\phi)=\wedge^{n_1+n_2}(\phi) \cong \wedge^{n_1}(\phi_1) \otimes \wedge^{n_2}(\phi_2)$$

But the tensor product $\wedge^{n_1}V_1 \otimes \wedge^{n_2}V_2$ is a one dimensional vector space and any linear endomorphism of such a space is given (in a basis) as multiplication with a number. Choosing a basis it follows the endomorphism $\wedge^{n_1}(\phi_1) \otimes \wedge^{n_2}(\phi_2)$ is multiplication with the number

$$\det(A_1)\det(A_2),$$

where $A_i$ is a matrix of $\phi_i$ in a basis $B_i$ for $V_i$.

Question: "But what about the determinant???"

By induction it follows that if $M$ is a matrix with square matrices $A_i$ along the diagonal, you get the formula

$$\det(M)=\det(A_1) \cdots \det(A_n).$$

Example: If $\phi$ is the matrix

\begin{align*} \phi= \begin{pmatrix} a & b \\ c & d \end{pmatrix} \end{align*}

and you view $\phi:V:=k\{e_1,e_2\} \rightarrow k\{e_1,e_2\}$ as a $k$-linear endomorphism ($k$ is a field), it follows by definition that

$$\wedge^2 \phi(e_1\wedge e_2)=\phi(e_1)\wedge \phi(e_2)= (ae_1+ce_2)\wedge (be_1+de_2)=(ad-bd)e_1 \wedge e_2:= $$

$$det(\phi)e_1 \wedge e_2.$$

Here we have used the property that $e_2 \wedge e_1=-e_1 \wedge e_2$ in the exterior product $\wedge^2 V$. More generally if $\phi:=(a_{ij})$ is an $n\times n$-matrix and $V:=k\{e_1,..,e_n\}$ with $\phi: V \rightarrow V$ it follows

$$\wedge^n \phi(e_1\wedge \cdots \wedge e_n):=\phi(e_1)\wedge \cdots \wedge \phi(e_n)=det(a_{ij})e_1\wedge \cdots \wedge e_n.$$

Taking the $n$'th exterior power of an $n \times n$-matrix $A$ is an "abstract" construction of the determinant $det(A)$.

Note: With this abstract definition of the determinant, it follows immediately that $det(AB)=det(A)det(B):$

Let $\phi:=(a_{ij}):=A, \psi:=(b_{ij}):=B$ be $n\times n$-matrices with coefficients $a_{ij},b_{ij}\in k$, viewed as endomorphisms of $V:=k\{e_1,..,e_n\}$. It follows

$$\wedge^n(\phi \circ \psi)(e_1\wedge \cdots \wedge e_n):= \phi(\psi(e_1))\wedge \cdots \wedge \phi(\psi(e_n))= $$

$$\wedge^n \phi(\psi(e_1)\wedge \cdots \wedge \psi(e_n))= \wedge^n \phi(\wedge^n \psi(e_1 \wedge \cdots \wedge e_n))$$

hence

$$\wedge^n (\phi \circ \psi)=\wedge^n \phi \circ \wedge^n \psi$$

and $det(AB)=det(A)det(B)$. This proof works over any commutative unital ring $k$.

You find other proofs here:

General expression for determinant of a block-diagonal matrix