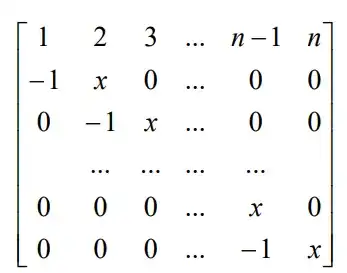How to compute this determinant

Question

I think adding some rows or column to each other will get a triangular matrix which is easy to compute but i cant see how

Answer 1

Proof:

I proceed by induction over n. After a while, if you try to calculate the determinant by rows reduction, you realize that the determinant seems to be $det(A) = \sum_{i=a_{11}}^{n} i\cdot x^{n-i}$ (where $a_{11}$ is the entry in the first row and first column of $A$).

So, for $n=2$ we have the matrix:

$$A = \left[\begin{matrix} 1 & 2 \\ -1 & x \end{matrix}\right]$$

It is easy to see that the determinant of this matrix is $x+2 = \sum_{i=1}^{2} i\cdot x^{2-i}$.

Now, suppouse the result for a matrix of shape $(n-1) \times (n-1)$. We have the matrix:

$$A = \left[\begin{matrix} 1 & 2 & 3 & \cdots & n-1 & n\\ -1 & x & 0 & \cdots & 0 & 0 \\ 0 & -1 & x & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & x & 0 \\ 0 & 0 & 0 & \cdots & -1 & x \end{matrix}\right]$$

So, if we apply reduction fixing the first column and visiting each row we have that:

$$det(A)= det(\hat{A}_{11}) + det(\hat{A}_{21}) $$

Where $\hat{A}_{ij}$ is the matrix resulting from crossing out row i and column j. Note that $\hat{A}_{11}$ is a lower triangular matrix of shape $(n-1) \times (n-1)$ and $\hat{A}_{21}$ is a matrix with the same form of the original matrix $A$, so we can apply the induction over $\hat{A}_{21}$ and obtain:

$$det(A)= x^{n-1} + \sum_{i=2}^{n} i\cdot x^{n-i} $$ $$det(A)= \sum_{i=1}^{n} i\cdot x^{n-i}$$

And with this result, the demonstration ends.

Answer 2

Proposition: Characteristic polynomial of the matrix $M=\begin{bmatrix} a_{n-1}&a_{n-2}&\ldots&a_{1}&a_0\\-1&0&\ldots&0&0\\0&-1&\ldots&0&0\\\vdots&\vdots&&\vdots&\vdots\\0&0&\ldots&-1&0 \end{bmatrix}$ is $(-x)^{n}+a_{n-1}(-x)^{n-1} +a_{n-2}(-x)^{n-2} +\ldots+a_0$.

Supposing the Proposition: Take $a_{n-1}=(1-x), a_{n-2}=2, \ldots, a_1=n-1, a_0=n$. Get that the determinant we are after is

$$x^n+(1-x)x^{n-1}+2x^{n-2}+\ldots+n=x^{n-1}+2x^{n-2}+\ldots+n.$$

Proof of the proposition (this is the companion matrix, up to some small changes of signs, so you may or may not need to read this proof): Let's see how $v=(v_0, \ldots,v_{n-1})$ can be an eigenvector. Applying the matrix to it, we get $Mv=(a_{n-1}v_0+a_{n-2}v_1+\ldots+a_0 v_{n-1}, -v_0, -v_1,\ldots, -v_{n-2})$. If this is an eigenvector with eigenvalue $\lambda=-\mu$ then

$$a_{n-1}v_0+a_{n-2}v_1+\ldots+a_0 v_{n-1}=-\mu v_0,$$ $$v_0=\mu v_1,$$ $$\ldots$$

$$v_{n-2}=\mu v_{n-1}.$$

Then we have $v_{n-1-k}=\mu^{k} v_{n-1}$ and

$$a_{n-1}\mu^{n-1} v_{n-1} +a_{n-2}\mu^{n-2} v_{n-1}+\ldots+a_0 v_{n-1}=-\mu^{n}v_{n-1} .$$

Of course, $v_{n-1}=0$ would lead to all $v_i$ being zero, which is not allowed. So we can divide out by $v_n$. Thus

$$\mu^{n}+a_{n-1}\mu^{n-1} +a_{n-2}\mu^{n-2} +\ldots+a_0=0.$$

Conversely, if the above equation holds, then $\lambda=-\mu$ is an eigenvalue (since we can take $v_{n-1}=1$ and reconstruct the eigenvector as $v=(\mu^{n-1}, \mu^{n-2}, \ldots, 1)$.)

So for all tuples $(a_{n-1}, \ldots, a_0)$ for which $(-x)^{n}+a_{n-1}(-x)^{n-1} +a_{n-2}(-x)^{n-2} +\ldots+a_0$ has distinct roots, it is the characteristic polynomial of $M$. But since coefficients of these are multivariable polynomials $a_0, \ldots, a_{n-1}$ they being equal on a dense set of $a$-tuples means that they are equal. This completes the proof.

Answer 3

\begin{align} \Delta_n&= \left|\begin{matrix} 1 & 2 & 3 & \cdots & n-1 & n\\ -1 & x & 0 & \cdots & 0 & 0 \\ 0 & -1 & x & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & x & 0 \\ 0 & 0 & 0 & \cdots & -1 & x \end{matrix}\right| \tag{1}\label{1} \end{align}

By expanding the determinant $\Delta_n$ with respect to the $n$-th column, we get a recurrence relation

\begin{align} \Delta_n&=x\cdot\Delta_{n-1}+(-1)^{n-1} n\cdot(-1)^{n-1} =x\cdot\Delta_{n-1}+n \end{align}
with initial condition $\Delta_1=1$, which has a solution in a compact form \begin{align} \Delta_n&=\frac{x(x^n-1)-n(x-1)}{(x-1)^2} \quad \text{for }\quad x\ne 1 \tag{2}\label{2} . \end{align}

In the limiting case for $x=1$ we have \begin{align} \Delta_n&=\lim_{x=1} \frac{x(x^n-1)-n(x-1)}{(x-1)^2} =\tfrac12n(n+1) \tag{3}\label{3} . \end{align}

Expression \eqref{2} can be also expressed in an expanded form as follows \begin{align} \Delta_n &=\frac{(x\sum_{k=0}^{n-1} x^k)-n}{x-1} \tag{4}\label{4} \\ &= \frac1{x-1}\sum_{k=1}^n (x^k-1) \tag{5}\label{5} \\ &= \sum_{k=1}^n \sum_{j=0}^{k-1} x^j = \sum_{k=1}^n k x^{n-k} \tag{6}\label{6} . \end{align}