What kind of mathematical spiral does the volute of an Ionic capital approximate?

Question

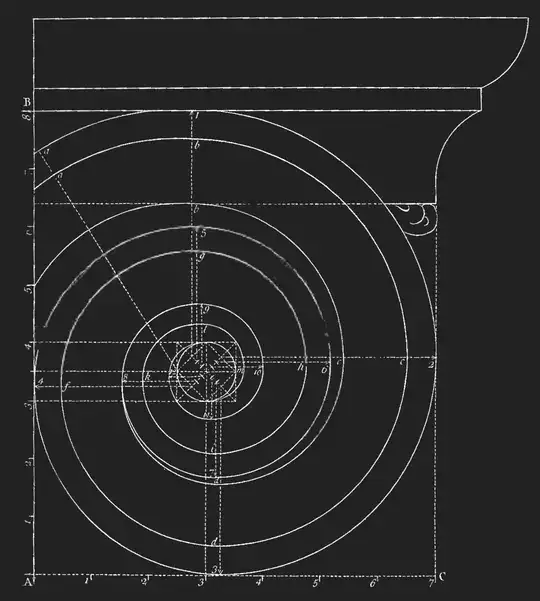
Ionic is one of the Classical Orders of architecture. A capital is the top portion of a column. The Ionic capital looks like this:

The spirals on either side are the volutes.

Various architects have given in-depth descriptions of how to draw these spirals, including Vignola in 1562 and Gibbs in 1753. In essence, their method looks like this:

Starting with a vertical line AB divided into 8 parts. Take 7 of these parts to create a horizontal line AC in order to describe a grid:

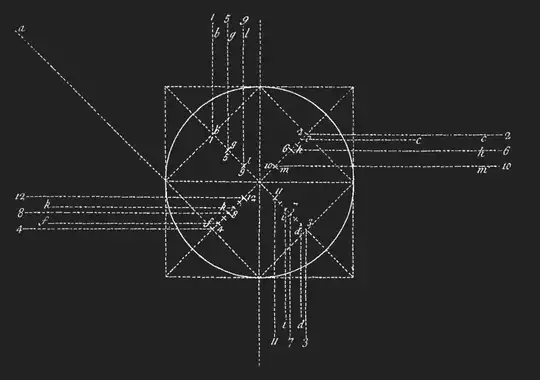
The eye is a circle whose diameter corresponds to one of these parts, and is placed as indicated above. A square rotated 45° is inscribed within the eye. It is bisected across the midpoints of its edges, and these bisectors are further divided into six equal parts:

Here is how you draw the spiral: You start with point 1 as the center of the circle, and follow it up to the top of the grid to get the initial radius. You draw this circle until it intersects the line 2.

Then you move the center to point 2, and draw until you hit line 3. Then you move the center to line 3 and draw until you hit line 4. This is repeated until your spiral intersects with the circle of the eye.

If that description wasn't sufficiently helpful, here is a video demonstrating (a slightly different version of) this technique.

My question is the following: Is this method of drawing a spiral meant to approximate a specific kind of mathematical spiral?

I know it's not Archimedean, but there are a bunch of other types of spiral. Which one of them is closest to this?

Answer 1

It's difficult to give a complete answer without knowing your mathematical background. That said, the answer to your question is that this spiral would fit in the category of polynomial spirals given by Dillen, F. (1990), "The Classification of Hypersurfaces of a Euclidean Space with Parallel Higher Order Fundamental Form," Mathematische Zeitschrift, 203: 635-643. (You should be able to find this article online.)

This is itself a generalization of the Cornu (aka Euler) spiral. I, myself, have created such spirals. However, for a quick and dirty example, you can take a Cornu spiral (solid line in the figure below) and apply the conjugate to the positive $x$ portion, as shown by the dashed line. The equation for the Cornu spiral is given here: Book about clothoids.

Answer 2

No is not one known mathematical shape that is sought. Merely all the methods devised (after 16th AD) were trying to approximate the archaic Greek ionic spiral volutes by using an easily reproducible tracing method that implicitly led to the realization of a particular shape, probably satisfactory both technically and aesthetically. I have spent some time in studying aprox. 100 different ancient ionic volute spirals (~9 th BC to 18 AD) and i can say that most of them are complex curves built out of circle arcs. different spirals of different temples of different locations scaled to same diameter There are rules behind the tracing of the spiral. However not always the same rules apply to different spirals but there are spirals belonging to different buildings that follow more or less the same rules. A while ago i wrote an article may be it helps (sry. french) https://www.persee.fr/doc/bch_0007-4217_2000_num_124_1_7265 but the domain is still able to produce many surprises.