If there is a sense in which $\liminf$ is a "concave" function, then we would expect Fatou's Lemma as a consequence of Jensen's inequality: Is there any way to make this precise?
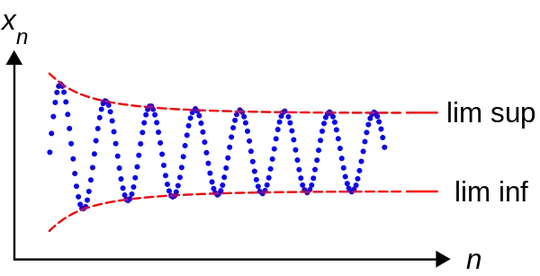
For a small example that shows I'm not entirely making this up, my intuition for $\limsup$ and $\liminf$ comes from the following picture (which is of one sequence of reals, but for functions we can imagine this picture happens pointwise):
Notice the $\limsup$ line curves in a "convex" way, and the $\liminf$ line curves in a "concave" way. Then, informally, we would expect (by Jensen's inequality):
$$\limsup \int f_n \leq \int \limsup f_n$$
$$\int \liminf f_n \leq \liminf \int f_n$$
Of course, these both agree with the correct inequalities based on Fatou's lemma.
I've looked around MSE for related questions (see here and here for example, though the first link is more interesting) but I haven't found any anything that addresses this in a satisfying way.
Is there any way to make this intuition precise?
Edit:
To give more context for making sense of this, we might view $\liminf$ as a function $\mathbb{R}^\mathbb{N} \to \mathbb{R}$. Then we curry $f_n(x)$ in the opposite order to the usual way. That is, we view it as associating to each $x \in \mathbb{R}$ a function $f_{-}(x) : \mathbb{N} \to \mathbb{R}$.
Now Fatou's lemma exactly says that $\int \liminf \circ f_{-}(x) d\mu(x) \leq \liminf \int f_{-}(x) d\mu(x)$, where one of our integrals is $\mathbb{R}^\mathbb{N}$ valued by defining $\left ( \int f_{-}(x) d\mu(x) \right )_n = \int f_{n}(x) d\mu(x)$.
I don't know if anyone has considered any machinery like this, if it is at all useful, etc. Which is why I'm asking this question
Thanks in advance!