Solving the following exercise I have some doubts. I want to show that \begin{equation*} \int_{0}^{\infty}\frac{\sin(x)}{x}dx=\frac{\pi}{2} \end{equation*}
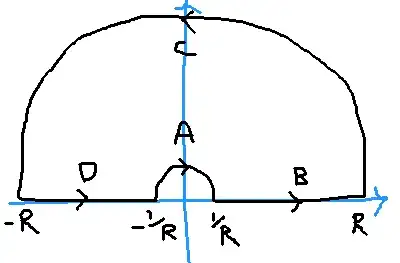
I tried the following: Let $\gamma$ be the upper semicircle \begin{equation*} \int_{\gamma} \frac{\sin(z)}{z} dz = 0 \end{equation*} how do we have to \begin{equation*} f(x) = \frac{\sin(x)}{x} = \frac{\sin(-x)}{-x} = f(-x) \end{equation*} Note that \begin{eqnarray*} 0 = \int_{\gamma} \frac{\sin(z)}{z} dz & = & \int_{-R}^{R} \frac{\sin(z)}{z} dz + \int_{C_{R}} \frac{\sin(z)}{z} dz\\ & = & \int_{-R}^{R} \frac{\sin(x)}{x} dx + \int_{C_{R}} \frac{\sin(z)}{z} dz\\ & = & 2\int_{0}^{R} \frac{\sin(x)}{x} dx + \int_{C_{R}} \frac{\sin(z)}{z} dz\\ \end{eqnarray*} then \begin{eqnarray*} -2 \int_{0}^{R} \frac{\sin(x)}{x}dx & = & \int_{C_{R}} \frac{\sin(z)}{z}dz\\ & = & \int_{0}^{\pi} \frac{\sin(Re^{i\theta})}{Re^{i\theta}} Rie^{i\theta} d\theta\\ & = & i\int_{0}^{\pi}\sin(Re^{i\theta})d\theta\\ & = & -\int_{u(0)}^{u(\pi)}\sin(u)udu\\ & = & -\left(u\cos(u)|_{u(0)}^{u(\pi)}-\int_{u(0)}^{u(\pi)}-\cos(u)du \right)\\ & = & -\left(Re^{i\theta}\cos(Re^{i\theta})|_{0}^{\pi}-\sin(Re^{i\theta})|_{0}^{\pi} \right)\to -\pi\text{ when }R\to\infty\text{ ?}\\ \end{eqnarray*} I do not think this last step is correct, however I see it necessary, I do not know if my reasoning is wrong or I should approach the problem from another point of view.
Is my reasoning correct? I have my doubts about being able to take the closed curve, because at $ z = 0 $ there is a singularity and it is located on the border of the region enclosed by my curve
PD: This requires the use of contour integral, although another method is also welcome