0

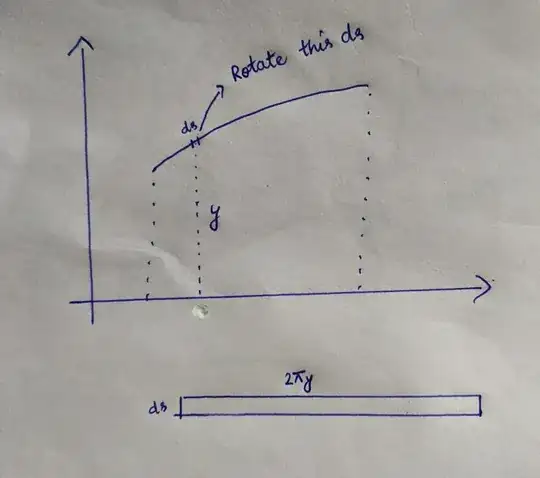
I learned from this pdf that the surface area of a revolution is $\int 2\pi y ds$. Why is it not $\int 2\pi y dx$?

I know this is a duplicated question, but I do not think I get a satisfactory answer. There is another pdf that told us the area under curve is $\int y dx$. Why are we using $dx$ in the area calculation, but not the surface area of a revolution?

Why can we use the argument that when the $\Delta x$ gets smaller and smaller, the limitation of $\sum y \Delta x$ is the area under curve, but we cannot use the same argument to the surface of a revolution? Why not say when the $\Delta x$ gets smaller and smaller, the limitation of $\sum 2\pi y \Delta x$ is the surface area of the revolution?

Dachuan Huang
  • 151
  • 1
    Thanks for pointing to that link. The "second order" vs "first order" argument helps a lot. However, let me ask a deeper (personal opinion :) ) question: why can we ignore the second order terms? Ignoring the second order term is also used at this pdf. I mean, we are supposed to do precise calculation instead of any level of approximation, right? – Dachuan Huang May 17 '21 at 06:37
  • The process of integration refines the answer to its exact form, I believe. – soupless May 17 '21 at 07:37
  • 1
    Does this answer your question : https://math.stackexchange.com/a/1692595/72031 – Paramanand Singh May 17 '21 at 10:14
  • @ParamanandSingh Thanks that helps a lot! I think it will be even more helpful if you can compare 2D area and 2D line length, because 2D is simpler than 3D. In your post, you are comparing 3D volume and 3D area. – Dachuan Huang May 18 '21 at 06:14
  • @ParamanandSingh I have one follow-up question that is beyond the territory of this problem. I know there is a difference between $\int \sqrt {1+ (y')^2} dx$ and $\int dx$ like what your post said. The difference $\Delta$ is a positive sum. However, why are we so sure that using a $ds$, a straight segment, is the right way to calculate the entire line length, why not other model, e.g. quadratic curve? – Dachuan Huang May 18 '21 at 06:19
  • @DachuanHuang: for arc-length the idea is simpler to deal with. Arc-length is by definition the limit of length of a polygonal arc. More details are available in this thread : https://math.stackexchange.com/a/3072835/72031 – Paramanand Singh May 18 '21 at 09:17
  • This link showed that we actually must prove the error goes to zero if we want to say two approximations are the same. This is a nice thing to keep in mind for newbies. Otherwise all approximations that look good are good. – Dachuan Huang May 18 '21 at 22:23

1 Answers1

0

First consider an element of thickness ds

When you rotate this ds element you will get a circle(you could say a ring with thickness ds also) of radius y and thickness ds

So when you just unfold this circle of thickness ds,you will get a rectangle whose length is equal to circumference 2πy,breadth is ds

Then you just integrate within the limits to get the required surface area

Main idea is you are calculating the area of surface and not the area under the curveenter image description here

I haven't done things rigorously,but just have given an intutive idea