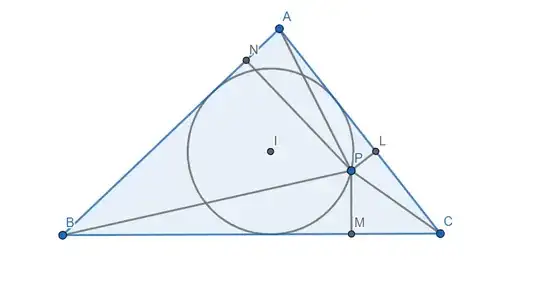
Prove that $PA^2\sin A + PB^2 \sin B + PC^2 \sin C$ takes the same value for all points P on the incircle of the triangle $\triangle ABC$.
The previous part asks that
If I is the incentre of the $\triangle ABC$ and $\alpha$, $\beta$, $\gamma$ are respectively the angles $BIC$, $CIA$ and $AIB$, prove that $$\frac{a \cdot IA}{\sin \alpha} = \frac{b \cdot IB}{\sin \beta} = \frac{c \cdot IC}{\sin \gamma}$$
And I have solve it with trigonometry, but I am not sure how to use it to prove the first statement. The general problem can be found here but I wonder if there is a simpler solution here since it only asks for points on the incircle. An idea is to use the fact that $$PA^2 \sin A = PA \cdot NL$$ etc. But I am not sure how to proceed.