Let us use the following :
For a point $P$ inside $\triangle{ABC}$,
$$\vec{OP}=\frac{[\triangle{PBC}]\cdot\vec{OA}+[\triangle{PCA}]\cdot\vec{OB}+[\triangle{PAB}]\cdot\vec{OC}}{[\triangle{ABC}]}\tag 1$$
where $[\triangle{PBC}]$ is the area of $\triangle{PBC}$.
Proof :
$\qquad\qquad\qquad\qquad$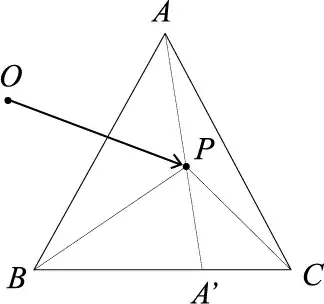
Since
$$\vec{OA'}=\frac{A'C\cdot \vec{OB}+BA'\cdot\vec{OC}}{A'C+BA'}=\frac{[\triangle{PCA}]\cdot\vec{OB}+[\triangle{PAB}]\cdot\vec{OC}}{[\triangle{PCA}]+[\triangle{PAB}]},$$
we have
$$\begin{align}\vec{OP}&=\frac{PA'\cdot\vec{OA}+AP\cdot\vec{OA'}}{PA'+AP}\\&=\frac{[\triangle{PBC}]\cdot\vec{OA}+([\triangle{PAB}]+[\triangle{PCA}])\cdot\vec{OA'}}{[\triangle{PBC}]+([\triangle{PAB}]+[\triangle{PCA}])}\\&=\frac{[\triangle{PBC}]\cdot\vec{OA}+[\triangle{PCA}]\cdot\vec{OB}+[\triangle{PAB}]\cdot\vec{OC}}{[\triangle{PBC}]+[\triangle{PCA}]+[\triangle{PAB}]}\\&=\frac{[\triangle{PBC}]\cdot\vec{OA}+[\triangle{PCA}]\cdot\vec{OB}+[\triangle{PAB}]\cdot\vec{OC}}{[\triangle{ABC}]}\end{align}$$
(By the way, $(1)$ holds for any point $P$ if we define the area of a "flipped" triangle as negative.)
For 1.
Let $I$ be the incenter.
Since $[\triangle{IBC}]:[\triangle{ICA}]:[\triangle{IAB}]=a:b:c$, by the law of sines, we have
$$\begin{align}\vec{PI}&=\frac{a\vec{PA}+b\vec{PB}+c\vec{PC}}{a+b+c}\\&=\frac{R\sin A\vec{PA}+R\sin B\vec{PB}+R\sin C\vec{PC}}{R\sin A+R\sin B+R\sin C}\\&=\frac{\sin A\vec{PA}+\sin B\vec{PB}+\sin C\vec{PC}}{\sin A+\sin B+\sin C}\end{align}$$where $R$ is the circumradius of $\triangle{ABC}$.
So, setting $k=\sin A+\sin B+\sin C$ gives
$$\vec{PI}=\frac{\sin A\vec{PA}+\sin B(\vec{AB}-\vec{AP})+\sin C(\vec{AC}-\vec{AP})}{k}=\frac{k\vec{PA}+\sin B\vec{AB}+\sin C\vec{AC}}{k}$$
$$\Rightarrow \vec{PA}=\vec{PI}-\frac{\sin B}{k}\vec{AB}-\frac{\sin C}{k}\vec{AC}.$$
Similarly, we have
$$\vec{PB}=\vec{PI}-\frac{\sin A}{k}\vec{BA}-\frac{\sin C}{k}\vec{BC},\quad\vec{PC}=\vec{PI}-\frac{\sin B}{k}\vec{CB}-\frac{\sin A}{k}\vec{CA}.$$
So, $$\small\begin{align}&PA^2\sin A+PB^2\sin B+PC^2\sin C\\&=\left(\vec{PI}-\frac{\sin B}{k}\vec{AB}-\frac{\sin C}{k}\vec{AC}\right)^2\sin A+\left(\vec{PI}-\frac{\sin A}{k}\vec{BA}-\frac{\sin C}{k}\vec{BC}\right)^2\sin B+\left(\vec{PI}-\frac{\sin B}{k}\vec{CB}-\frac{\sin A}{k}\vec{CA}\right)^2\sin C\\&=kPI^2+\left(-2\sin A\sin B(\vec{AB}+\vec{BA})-2\sin B\sin C(\vec{BC}+\vec{CB})-2\sin C\sin A(\vec{AC}+\vec{CA})\right)\cdot\frac{\vec{PI}}{k}+s\\&=(\sin A+\sin B+\sin C)PI^2+s\end{align}$$
where $s$ is a constant independent from $P$.
So, $PA^2\sin A+PB^2\sin B+PC^2\sin C$ is minimum if $P=I$.
For 2.
Let $H$ be the orthocenter.
Since $[\triangle{HCA}]:[\triangle{HAB}]=A'C:BA'=\frac{AA'}{\tan C}:\frac{AA'}{\tan B}=\tan B:\tan C$ where $A'$ is on the side $BC$ such that $AA'$ is perpendicular to $BC$, we have
$$[\triangle{HBC}]:[\triangle{HCA}]:[\triangle{HAB}]=\tan A:\tan B:\tan C.$$
So, $$\vec{PH}=\frac{\tan A\vec{PA}+\tan B\vec{PB}+\tan C\vec{PC}}{\tan A+\tan B+\tan C}.$$
By the similar argument as the one in the first, we can have
$$PA^2\tan A+PB^2\tan B+PC^2\tan C=(\tan A+\tan B+\tan C)PH^2+t$$
where $t$ is a constant independent from $P$.
Thus, $PA^2\tan A+PB^2\tan B+PC^2\tan C$ is minimum if $P=H$.
For 3.
Let $G$ be the centroid.
We have $$\vec{PG}=\frac{\vec{PA}+\vec{PB}+\vec{PC}}{3}.$$
So, $$\vec{PA}=\vec{PG}-\frac{\vec{AB}+\vec{AC}}{3},\quad\vec{PB}=\vec{PG}-\frac{\vec{BA}+\vec{BC}}{3},\quad\vec{PC}=\vec{PG}-\frac{\vec{CB}+\vec{CA}}{3}.$$
Hence, we have
$$\begin{align}&PA^2+PB^2+PC^2\\&=\left(\vec{PG}-\frac{\vec{AB}+\vec{AC}}{3}\right)^2+\left(\vec{PG}-\frac{\vec{BA}+\vec{BC}}{3}\right)^2+\left(\vec{PG}-\frac{\vec{CB}+\vec{CA}}{3}\right)^2\\&=3PG^2+u\end{align}$$
where $u$ is a constant independent from $P$.
Thus, $PA^2+PB^2+PC^2$ is minimum if $P=G$.
For 4.
Let $O$ be the circumcenter.
Since $$\begin{align}[\triangle{OBC}]:[\triangle{OCA}]:[\triangle{OAB}]&=\frac{R^2\sin(2A)}{2}:\frac{R^2\sin(2B)}{2}:\frac{R^2\sin(2C)}{2}\\&=\sin(2A):\sin(2B):\sin(2C),\end{align}$$
we have $$\vec{PO}=\frac{\sin(2A)\vec{PA}+\sin(2B)\vec{PB}+\sin(2C)\vec{PC}}{\sin(2A)+\sin(2B)+\sin(2C)}.$$
By the similar argument as the one in the first, we have
$$PA^2\sin(2A)+PB^2\sin(2B)+PC^2\sin(2C)=(\sin(2A)+\sin(2B)+\sin(2C))PO^2+v$$
where $v$ is a constant independent from $P$.
Thus, $PA^2\sin(2A)+PB^2\sin(2B)+PC^2\sin(2C)$ is minimum if $P=O$.
