3

I have 5 points of a conic. And a given line. I have to construct from these the intersection(s) of the conic and the line. From 5 points I can construct more points of the conics. But I am not sure how to construct the points of the intersection of the conic (given by 5 points only) and the line. Could you help me construct their intersection?

  • "Construct" as in geometric construction, or is building the conic equation first and solving allowed? – Parcly Taxel May 10 '21 at 17:39
  • Cross reference: see https://math.stackexchange.com/a/867428/35416 for an algebraic approach. I see you are looking for a construction instead, so this is a related but different question. – MvG May 10 '21 at 17:47
  • @ParclyTaxel I meant geometric construction. –  May 10 '21 at 18:21
  • From five points you can construct foci and vertices of the conic. The positions of the projections of the intersection points on the major axis are the solutions of a quadratic equation, hence constructible with ruler and compass. But this might not be that kind of "nice" construction you are looking for. – Intelligenti pauca May 10 '21 at 20:36
  • @Intelligentipauca I think it would be a great answer. I did not think of this construction, but I would be grateful if you expounded it. I started differently by making a $PA_i \rightarrow QA_i$ compliance between the points of the conic. –  May 10 '21 at 20:45

2 Answers2

3

Projective geometry textbooks from the 19th and early 20th centuries are the best place to find recipes for constructions like this.

The basic idea is to construct an involution on the line, the fixed points of which are the points of intersection of the line and conic.

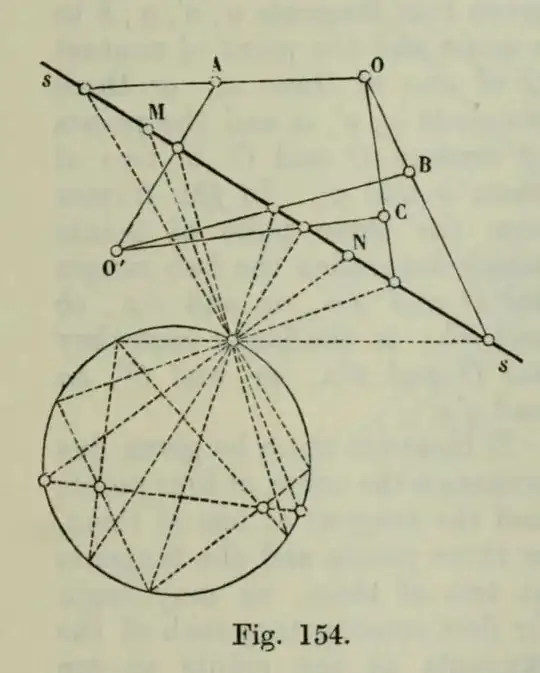
One such construction is given in Cremona, Projective Geometry, Art. 212 (pg 211). You'll notice it's more work than finding more points on the conic, but it'll expand your toolkit of constructions.

(Here's a cleaner copy)

The excerpted diagram below shows the five points $O,O',A,B,C$ that define the conic, along with the line $s$. The points $M,N$ are the points of intersection of the line and conic, and are constructed via a reverse and forward stereographic projection to and from a circle. How cool is that?

enter image description here

brainjam
  • 8,626
3

Let's assume your five points lie in the $xy$-plane. Then we can express them as $P_i = (x_i, y_i)$, $i=1,2,3,4,5$. Then the equation of the conic passing through them is: $$ \left| \matrix{ x^2 & y^2 & xy & x & y & 1 \\ x_1^2 & y_1^2 & x_1y_1 & x_1 & y_1 & 1 \\ x_2^2 & y_2^2 & x_2y_2 & x_2 & y_2 & 1 \\ x_3^2 & y_3^2 & x_3y_3 & x_3 & y_3 & 1 \\ x_4^2 & y_4^2 & x_4y_4 & x_4 & y_4 & 1 \\ x_5^2 & y_5^2 & x_5y_5 & x_5 & y_5 & 1 } \right| = 0 $$

Now suppose our line passes through the point $(a,b)$ and its direction is given by the vector $(u,v)$. Then its parametric equations can be written: $$ x = a + tu \\ y = b + tv $$ The intersection of the line with the ellipse occurs at $t$ values that satisfy $$ \left| \matrix{ (a + tu)^2 & (b + tv)^2 & (a + tu)(b + tv) & a + tu & b + tv & 1 \\ x_1^2 & y_1^2 & x_1y_1 & x_1 & y_1 & 1 \\ x_2^2 & y_2^2 & x_2y_2 & x_2 & y_2 & 1 \\ x_3^2 & y_3^2 & x_3y_3 & x_3 & y_3 & 1 \\ x_4^2 & y_4^2 & x_4y_4 & x_4 & y_4 & 1 \\ x_5^2 & y_5^2 & x_5y_5 & x_5 & y_5 & 1 } \right| = 0 $$

This is a quadratic equation in $t$, which you can easily solve to get the $t$ values at the intersections (if any). Then you substitute these $t$ values back into the line equation to get the points of intersection.

bubba
  • 43,483
  • 3
  • 61
  • 122
  • 1
    Here's an idea. Suppose you are given the five points and a line on an otherwise blank sheet of paper. You can take the line as the $x$-axis, construct a perpendicular to make the $y$-axis, then define the coordinates of the five points by construction. Put those values into your determinantal equation for the conic and then render $y=0$ to get the coordinates of the intersection points along the line. Inelegant, but it works. – Oscar Lanzi May 17 '21 at 00:01
  • Yes. This amounts to choosing a coordinate system in which $(a,b) = (0,0)$ and $(u,v)= (1,0)$. This will simplify the determinant, of course. Alternative, if you want to, you can choose a coordinate system in which two of the $y_i$ are zero and one of the $x_i$ is zero. This will again simplify the determinant equation. – bubba May 17 '21 at 00:40
  • The rendering approach will only give you answers at the resolution of the rendering. Don’t know if that’s good enough for your application. It’s definitely not good enough for the ones I work on. – bubba May 17 '21 at 00:42
  • Well, that kills that. (Your second comment.) – Oscar Lanzi May 17 '21 at 00:45