Here's an attempted explanation for why there are extra steps. The short version is that even though projective geometry has a duality principle, the game of straightedge construction is rigged against one side of the duality.
For the polar->pole construction, let's dualize the construction you gave for pole->polar.
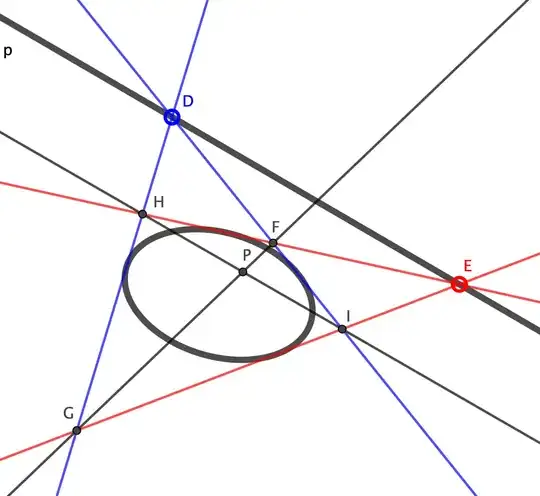
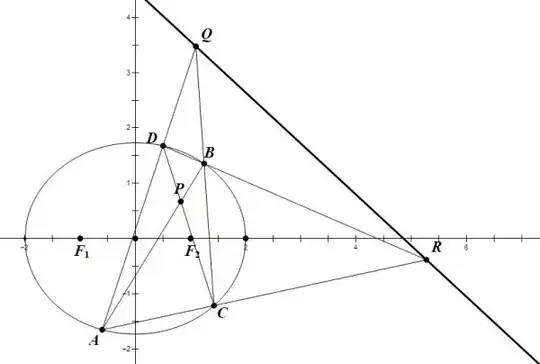
Starting with the conic and line $p$, select points $D,E$ on $p$ and draw tangents to the conic. Find the four intersections of the four tangents - $F,G,H,I$. Then the pole $P$ is the intersection of $FG\cap HI$. Voila, we've drawn seven lines to get the pole.
But, you object, we can't just pull the four tangents out of a hat. They have to be constructed using the polars of $D$ and $E$, at a cost of several more lines.
The counter argument to this is that in the pole->polar construction, we're assuming that the conic has been drawn explicitly and accurately. Maybe that's a bad assumption, and we need to construct the intersection points explicitly, based on the five points defining the conic, as in this answer. That would make for a much longer construction.
In a world of perfect duality, drawing a tangent to a conic from a point should be just as easy as intersecting a line and a conic. Drawing a tangent from a point could be considered as selecting a line from a line conic, which is dual to selecting a point on a point conic.
This is true in, say, Geogebra, where constructing a tangent is a primitive, on the same level as finding an intersection. But in the world of straight edge and paper the rules work against this equivalence. We take for granted that we can draw a line through a conic and pick out the intersections, but we don't accept that we can do the dual task of finding a tangent from a point in a single step.
The deal breaker is that in straightedge constructions we think of the point conic locus as a given, while that's not true of the line conic, because it is impossible to draw and work with the lines which form the envelope.