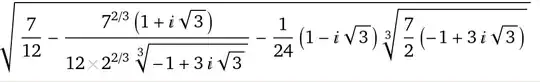Technically, every value of sin can be expressed in closed form by means of using the exponential definition of sine:
$$\mathrm{sinθ=\frac{e^{iθ}-e^{-iθ}}{2i}}$$
Simply substitute the value of θ wanted and you will get a form in terms of the natural base exponential function
I assume you probably mean for θ=qπ,$ q\in \Bbb Q$. In this case, the sine can be written in terms of a polynomial root in which case wikipedia considers closed form solutions, even though a general formula for degree 5 and above is impossible using finite numbers radicals, arithmetic operations, and integers where the imaginary unit can be expressed by the square root and the integer -1. Even this is true:
$$\mathrm{sin\frac π7=a\ root(64x^6-112x^4+56x^2-7)}=$$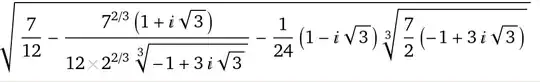
This result was gotten using Mathematica, which would be quite the pain to type out, but still shows how complex these answers can get using complex numbers...
As seen by from Wikipedia
In mathematics, a closed-form expression is a mathematical expression expressed using a finite number of standard operations. It may contain constants, variables, certain "well-known" operations (e.g., + − × ÷), and functions (e.g., nth root, exponent, logarithm, trigonometric functions, and inverse hyperbolic functions), but usually no limit, differentiation, or integration. The set of operations and functions admitted in a closed-form expression may vary with author and context.
If you want even more specific answers, if you do not consider the root function, for which the polynomial has no closed form in terms of finite radicals, integers, and arithmetic operations, then one should consider composite numbers, and certain prime numbers as mentioned nicely in another answer. These prime numbers are Fermat Primes for which I am not sure why these are the only ones for trigonometric functions.
Nevertheless, if a number can be decomposed into a its prime factorization in terms of Fermat Primes and 2, then it seems that the trigonometric function does have a value. The numerator can then be evaluated, after the form of θ=$\frac{\pi}{r\in \Bbb N}$ using multiple angle formulas and making θ=$\mathrm{\frac{π}{r}⇔x=rθ}$, through multiple angle formulas. Also, the even and odd properties can be used to determine the answer based in the sign of the argument. Sorry for one of my answers, but this
Link to the Answer is a Great Example This Process..