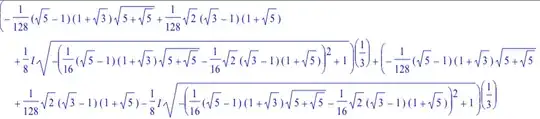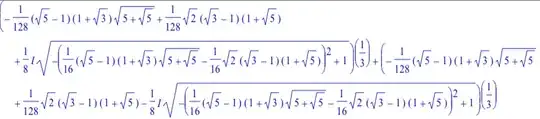I do not catch exactly what is your problem, so I am proposing some considerations which might be useful,
at least to substantiate what you need.
a) The sine of an angle will be rational when the angle corresponds to that of an integral triangle (i.e. a Pythagorean triple).
Among the angles which are rational multiples of $\pi$, only $0, \pi /6 , \pi /2 (+ k \pi)$ provide a rational value of the sine.
see this reference.
And if the angle is a rational multiple of $\pi$ it is as well a rational multiple of $180^{\circ}$ and thus a rational value in degrees.
Therefore the sines you are looking for are irrational.
b) The methods for finding a rational approximation of a (irrational) $\sin x$ are various, and are the subject
of the hard work of many scholars of the past, when the trigonometric tables were much of need
and the computer was far to come.
An example is the Bhaskara sine approximation.
$$
\sin x^ \circ \approx
{{4x\left( {180 - x} \right)} \over {40500 - x\left( {180 - x} \right)}}
$$
which for one of the angles you cite as example will give
$$
\eqalign{
& x = \left( {{{143} \over 3}} \right)^{\, \circ }
= \left( {{{143} \over {540}}} \right)\pi \;rad\quad \Rightarrow \cr
& \Rightarrow \quad \sin x \approx {{227084} \over {307729}} \to err = 0.17\,\% \cr}
$$
And when the computer arrived, also there has been much work to find suitable algorithms to express the trig functions which are summarized in this Wikipedia article .
There it is stated that the sine of rational multiples of $\pi$ are in fact algebraic numbers (generally of degree $2$ and higher).
A recent paper illustrates a rational approximation for the $\tan$ and for $\sin , \cos$ functions.
c) However most of the algorithms developed for being implemented on computers relies on the angle expressed in radians,
and therefore they will provide a rational approximation of the sine when the angle is expressed as a rational multiple of a radian.
The problem that you pose concerns instead the sine of an angle expressed as a fraction of degrees, which is irrational in radians.
Aside from the Bhaskara's formula above, with the other available methods you cannot avoid to introduce
a rational approximation for $\pi$, which is going to fix the threshold on the precision that can be achieved.
To this end we would better fix some lower/upper couple of bounds on $\pi$ such as
$$
\left( {{{25} \over 8},{{22} \over 7}} \right),\left( {{{91} \over {29}},{{22} \over 7}} \right),
\cdots ,\left( {{{688} \over {219}},{{355} \over {113}}} \right), \cdots ,
\left( {{{9918} \over {3157}},{{355} \over {113}}} \right), \cdots
$$
obtainable by a Stern-Brocot approximation.
Then if you are using the Taylor series, for instance, you have
$$
x - {1 \over 6}x^{\,3} < \sin x < x - {1 \over 6}x^{\,3} + {1 \over {120}}x^{\,5}
$$
so that for the angle already considered
$$
x = \left( {{{143} \over 3}} \right)^{\, \circ } = \left( {{{143} \over {540}}} \right)\pi \;rad
$$
and using for $\pi$ the second couple of values above, you get
$$
\left( {{{143} \over {540}}{{91} \over {29}}} \right)
- {1 \over 6}\left( {{{143} \over {540}}{{91} \over {29}}} \right)^{\,3}
< \sin x <
\left( {{{143} \over {540}}{{22} \over 7}} \right)
- {1 \over 6}\left( {{{143} \over {540}}{{22} \over 7}} \right)^{\,3}
+ {1 \over {120}}\left( {{{143} \over {540}}{{22} \over 7}} \right)^{\,5}
$$
i.e.
$$
{{16943907583603} \over {23042336976000}} < \sin x < {{2140128005530465093} \over {2893944959388000000}}
$$
which put into decimal is
$$
0.735338 \ldots < 0.739239 \ldots < 0.7395132 \ldots
$$
corresponding to a relative error of
$$
- \,0.5\,\% \,,\; + 0.04\,\%
$$
Of course , depending on the accuracy required, it is possible to increase the precision on $\pi$, increase the degree of the
series, or also to change to Padè approximants or other techniques.