Limit of infinite composition of sin(x)

Question

I was playing around on desmos the other day, and noticed that $\sin\left(\sin\left(x\right)\right)$ is basically a version of sin with a lower amplitude (which makes intuitive sense). To me, it seems intuitve that this curve, when composed infinite times, becomes a straight line, as the values at $x=\frac{\pi}{2}\mathbb{Z}$ would move (slowly) towards the values at $x=\pi\mathbb{Z}$ by virtue of them moving away from the peaks, but is there a way to go about properly proving this?

Answer 1

Good question. The straight line you are talking about is actually the line $y=0$.

One way to see this is to start at any point $x_0\in\mathbb{R}$ and apply a fixed point iteration with the formula $$x_{n+1} = \sin(x_n).$$

It's almost as if the maths Gods knew you were going to ask this question, because Wikipedia even has a nice diagram of what's going on in your exact example!

The diagram shows what happens with $x_0 = 2$. You get a staircase diagram converging towards the only root of the equation $x = \sin(x),\ $ namely $x = 0.$

But this was with a starting point of $x_0 = 2.$ What about other starting points? Well, we know that, for all $x \in \mathbb{R},\ -1 \leq \sin(x) \leq 1.$ If $x_0$ is such that $0\leq x_1=\sin(x_0)\leq 1,\ $ then we get a convergence similar to that in the diagram above (staircase). And if $x_0$ is such that $-1\leq x_1=\sin(x_0)\leq 0,\ $ then we also get something similar, but happening below the $x-$axis, but still towards the root $x=0$.

It follows that the curve that $\sin\left(\sin\left(\sin\left(\ldots x \right)\right)\right)$ converges to is in fact the $x$-axis, ie. the line $y=0.$

Why/when does this occur / how can we prove that we get convergence via this "fixed-point iteration" process?

It can be shown that a fixed-point iteration $x_{n+1} = g(x_n)$:

• converges if $\ \vert g'(x)\vert < 1\ $ near the root and $x_1$ is sufficiently close to the root
• diverges if $\ \vert g'(x) > 1\ $ near the root.

There's lots of material out there if you want to look up proofs of these things, but the above is a summary of when convergence happens.

In the $x_{n+1} = \sin(x_n)\ $ example, we have $g(x)=\sin(x).\ $ We know that $g'(0) = 1$, and $g'(x)<1$ for $x$ close to but not equal to the root. We have also seen that $x_1\in [-1,1]\ $ and is sufficiently close to the root. Therefore we get convergence towards $0$ for any starting value $x_0.$

Answer 2

Evaluation of the Limit

Let $a_{n+1}=\sin(a_n)$ and suppose $a_0\gt0$.

As shown in this answer, for $x\gt0$, $0\lt\sin(x)\lt x$. Thus, $a_n$ is a decreasing sequence bounded below by zero. Therefore, $\lim\limits_{n\to\infty}a_n$ exists. Since $\sin(x)$ is continuous, $$ \begin{align} \lim_{n\to\infty}a_n &=\lim_{n\to\infty}\sin(a_n)\tag{1a}\\ &=\sin\left(\lim_{n\to\infty}a_n\right)\tag{1b} \end{align} $$ Since $\sin(x)=x$ only at $x=0$, $(1)$ says that $$ \bbox[5px,border:2px solid #C0A000]{\lim_{n\to\infty}a_n=0}\tag2 $$ Since $\sin(x)$ is an odd function, $(2)$ holds for $a_0\lt0$.

Of course, if $a_0=0$, then $a_n=0$ for all $n\ge0$, and $(2)$ holds for $a_0=0$.

---

Asymptotics

As shown in this answer $$ \lim\limits_{x\to0}\frac{x-\sin(x)}{x^3}=\frac16\tag3 $$ If $a_0\ne0$, since $a_{n+1}=\sin(a_n)$, $(2)$ and $(3)$ say $$ \lim_{n\to\infty}\frac{a_n-a_{n+1}}{a_n^3}=\frac16\tag4 $$ An immediate consequence of $(2)$ and $(4)$ is $$ \begin{align} \lim_{n\to\infty}\frac{a_{n+1}}{a_n} &=\lim_{n\to\infty}\left(1-a_n^2\frac{a_n-a_{n+1}}{a_n^3}\right)\tag{5a}\\ &=1-0^2\cdot\frac16\tag{5b}\\[6pt] &=1\tag{5c} \end{align} $$ Thus, $(4)$ and $(5)$ give $$ \begin{align} \lim_{n\to\infty}\left(\frac1{a_{n+1}^2}-\frac1{a_n^2}\right) &=\lim_{n\to\infty}\frac{a_n^2-a_{n+1}^2}{a_n^2a_{n+1}^2}\tag{6a}\\ &=\lim_{n\to\infty}\frac{a_n-a_{n+1}}{a_n^3}\lim_{n\to\infty}\frac{a_n+a_{n+1}}{a_{n+1}}\lim_{n\to\infty}\frac{a_n}{a_{n+1}}\tag{6b}\\ &=\frac16\cdot2\cdot1\tag{6c}\\[3pt] &=\frac13\tag{6d} \end{align} $$ Finally, Stolz-Cesàro and $(6)$ say that $\lim\limits_{n\to\infty}\frac1{na_n^2}=\frac13$; that is, $$ \bbox[5px,border:2px solid #C0A000]{\lim_{n\to\infty}na_n^2=3}\tag7 $$ In fact, starting with $a_0=1$, we get $$ \begin{array}{r|l} n&na_n^2\\\hline 1&0.7080734183\\ 10&2.1433001582\\ 100&2.8511162950\\ 1000&2.9803925383\\ 10000&2.9976147637\\ 100000&2.9997198782\\ 1000000&2.9999678410 \end{array} $$

---

Bounds

Substituting $x\mapsto x/\pi$ in $(7)$ from this answer, we get $$ \cot(x)=\sum_{k\in\mathbb{Z}}\frac1{k\pi+x}\tag8 $$ Subtracting $(8)$ from $\frac1x$ and taking the derivative, we get $$ \frac1{\sin^2(x)}-\frac1{x^2}=\sum_{\substack{k\in\mathbb{Z}\\k\ne0}}\frac1{(k\pi+x)^2}\tag9 $$ Evaluating $(9)$ at $x=0$ gives $\frac2{\pi^2}\zeta(2)=\frac13$, which agrees with $(6)$.

Taking two derivatives of $(9)$ gives $$ \begin{align} \frac{\mathrm{d}^2}{\mathrm{d}x^2}\left(\frac1{\sin^2(x)}-\frac1{x^2}\right) &=\sum_{\substack{k\in\mathbb{Z}\\k\ne0}}\frac6{(k\pi+x)^4}\\ &\ge0\tag{10} \end{align} $$ Thus, $\frac1{\sin^2(x)}-\frac1{x^2}$ is an even convex function with a minimum of $\frac13$ at $x=0$.

Since $a_k^2$ is decreasing, $$ \frac13\le\frac1{a_{k+1}^2}-\frac1{a_k^2}\le\frac1{\sin^2(a_0)}-\frac1{a_0^2}\tag{11} $$ Summing $(11)$ gives $$ \frac n3\le\frac1{a_n^2}-\frac1{a_0^2}\le n\left(\frac1{\sin^2(a_0)}-\frac1{a_0^2}\right)\tag{12} $$ Since $\sin^2(x)\le1$, assume that $a_0^2\le1$, whence $\frac1{\sin^2(a_0)}-\frac1{a_0^2}\le\cot^2(1)$.

Solving $(12)$ for $a_n^2$ yields $$ \frac{\tau a_0^2}{\tau+na_0^2}\le a_n^2\le\frac{3a_0^2}{3+na_0^2}\tag{13} $$ where $\tau=\tan^2(1)\approx2.42551882$.

---

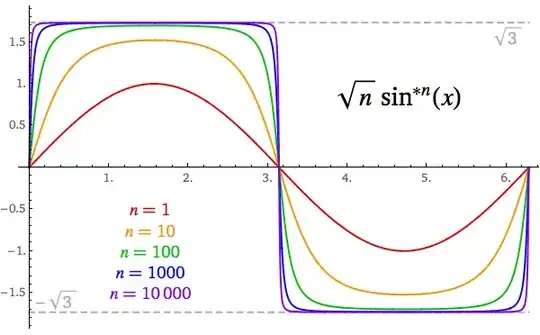
Graphical Verification

Limit $(7)$ holds for any $a_0\ne0$. Since $\sin(x)$ is an odd function, changing the sign of $a_0$, changes the sign of all $a_n$. Thus, we have that $$\newcommand{\sgn}{\operatorname{sgn}} \lim_{n\to\infty}\sqrt{n}\,a_n=\sqrt3\sgn(a_0)\tag{14} $$ Therefore, if we define $\sin^{\ast n}(x)$ to be the $n$-fold composition of $\sin(x)$, we get $$ \bbox[5px,border:2px solid #C0A000]{\lim_{n\to\infty}\sqrt{n}\sin^{\ast n}(x)=\sqrt3\sgn(\sin(x))}\tag{15} $$ Here is graphical verification of $(15)$:

Asymptotically, $(15)$ says that $$ \bbox[5px,border:2px solid #C0A000]{\sin^{\ast n}(x)\sim\sqrt{\frac3n}\sgn(\sin(x))}\tag{16} $$ which would be a more precise way of saying what you were trying to say.

Answer 3

We know that $\sin(\mathbb{R})=[-1,1]$ Since the sine function is odd, it will be enough to consider the interval $[0,1]$. The sine function is increasing on this interval so $\sin([0,1])=[0,\sin(1)]$ Since $|sin(x)|<|x|$ this will be a shorter interval than $[0,1]$. We can apply the process repeated getting a succession of smaller intervals, which must either converge to the origin, or to an interval $[0,y]$ with $y=\sin y$. But the only such $y$ is $y=0$, and the intervals shrink to the origin.

Thus, for any $\varepsilon>0$ there is $N$ such for $n>N,\ |\sin^{(n)}x|<\varepsilon$ for every $x\in \mathbb{R}$. Thus, you are correct in saying that the graph will look like a straight line, in fact the $x$-axis.

Answer 4

This is straightforward to prove, but needs attention to some detail.

Suppose we pick some $x_0$ and let $x_{n+1} = \sin x_n$. The idea is to show that $x_n \to 0$.

If $x_0 = 0$ then $x_n = 0 $ for all $n$, so suppose $x_0 \neq 0$. Note that $|x_n| \le 1$ for $n \ge 1$, so we might as well suppose $|x_0| \le 1$.

The mean value theorem shows that for for $x \neq 0$ and $|x| \le 1$ that $\sin x-0 = (\cos \xi) x$ for some $\xi \in (0, x)$ (or $(x,0)$ if $x <0$), and since $\cos \xi \in (\cos 1,1)$ (using $x\neq0$ and $|x| \le 1$ here) we see that $|\sin x| = \sin |x| < |x|$.

In particular, $|x_n| $ is non increasing and so $|x_n| \to t^*$ for some $t^*$. By continuity we have $\sin t^* = t^*$ and from the previous paragraph we see that we must have $t^* = 0$. Hence $x_n \to 0$ always.