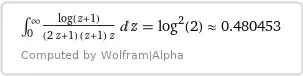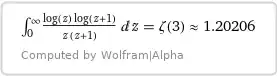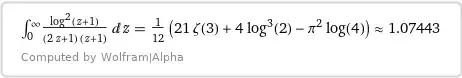Evaluate $\int _0^{\frac{\pi }{2}}x\cot x\ln ^2(\cos x)\:dx$

Question

I want to evaluate $$\int _0^{\frac{\pi }{2}}x\cot (x)\ln ^2(\cos x)\:dx $$ but it's quite difficult. I have tried to rewrite the integral as $$\int _0^{\frac{\pi }{2}}x\cot \left(x\right)\ln ^2\left(\cos \left(x\right)\right)\:dx=\frac{\pi }{2}\int _0^{\frac{\pi }{2}}\tan \left(x\right)\ln ^2\left(\sin \left(x\right)\right)\:dx-\int _0^{\frac{\pi }{2}}x\tan \left(x\right)\ln ^2\left(\sin \left(x\right)\right)\:dx$$ I've also tried to integrate by parts in multiple ways yet I cant go forth with this integral, I also tried using the substitution $t=\tan{\frac{x}{2}}$ but cant get anything to work, I'll appreciate any sort of help.

I also tried using the classical expansion $$\ln \left(\cos \left(x\right)\right)=-\ln \left(2\right)-\sum _{n=1}^{\infty }\frac{\left(-1\right)^n\cos \left(2nx\right)}{n},\:-\frac{\pi }{2}<x<\frac{\pi }{2}$$ But it only gets worse.

Answer 1

$$I=\frac{1}{2}\int_0^{\pi/2} x^2\frac{\ln^2\cos x}{\sin^2x} \, dx+\int_0^{\pi/2} x^2{\ln\cos x}\,dx$$ integrating by parts $$\int_0^{\pi/2} x^2 \ln\cos x \, dx=\frac{\pi^3}{24}\ln2-\frac{\pi}{4}\zeta(3)$$ see Integral $\int_0^\pi \theta^2 \ln^2\big(2\cos\frac{\theta}{2}\big)d \theta$. $$I=\int_0^{\pi/2} x^2\frac{\ln^2\cos x}{\sin^2x} \, dx = \frac{1}{4} \int_0^\infty\frac{(\arctan u)^2 \log^2(1+u^2)}{u^2} \, du$$ Put $$x=\arctan u$$

Closer form for $\int_0^\infty\frac{(\arctan{x})^2\log^2({1+x^2})}{x^2}dx$

Answer 2

My approach. $$\int _0^{\frac{\pi }{2}}x\cot \left(x\right)\ln ^2\left(\cos \left(x\right)\right)\:dx$$

$$=\frac{1}{4}\int _0^{\infty }\frac{\arctan \left(x\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx=\frac{\pi }{8}\int _0^{\infty }\frac{\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx$$ $$-\frac{1}{4}\int _0^{\infty }\frac{\arctan \left(\frac{1}{x}\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx$$

---

$$\int _0^{\infty }\frac{\arctan \left(\frac{1}{x}\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx=\frac{\pi }{2}\int _0^{\infty }\frac{x\ln ^2\left(\frac{x^2}{1+x^2}\right)}{1+x^2}\:dx-\int _0^{\infty }\frac{x\arctan \left(\frac{1}{x}\right)\ln ^2\left(\frac{x^2}{1+x^2}\right)}{1+x^2}\:dx$$ $$=\frac{\pi }{2}\int _0^{\infty }\frac{x\ln ^2\left(\frac{x^2}{1+x^2}\right)}{1+x^2}\:dx-\frac{4}{3}\int _0^{\infty }\frac{x\arctan ^3\left(\frac{1}{x}\right)}{1+x^2}\:dx-\frac{4}{3}\operatorname{\mathfrak{I}} \left\{\int _0^{\infty }\frac{x\ln ^3\left(\frac{x}{x-i}\right)}{1+x^2}\:dx\right\}$$ $$=\frac{\pi }{4}\int _0^1\frac{\ln ^2\left(x\right)}{1-x}\:dx+4\int _0^{\frac{\pi }{2}}x^2\ln \left(\sin \left(x\right)\right)\:dx-\frac{4}{3}\operatorname{\mathfrak{I}} \left\{3\operatorname{Li}_4\left(2\right)+i\pi \ln ^3\left(2\right)-6\zeta \left(4\right)\right\}$$ $$=\frac{5\pi }{4}\zeta \left(3\right)-\frac{\pi ^3}{6}\ln \left(2\right)-\frac{2\pi }{3}\ln ^3\left(2\right)$$

---

Thus. $$\frac{1}{4}\int _0^{\infty }\frac{\arctan \left(x\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx=\frac{\pi }{8}\zeta \left(3\right)-\frac{1}{4}\left(\frac{5\pi }{4}\zeta \left(3\right)-\frac{\pi ^3}{6}\ln \left(2\right)-\frac{2\pi }{3}\ln ^3\left(2\right)\right)$$ Therefore. $$\int _0^{\frac{\pi }{2}}x\cot \left(x\right)\ln ^2\left(\cos \left(x\right)\right)\:dx=-\frac{3\pi }{16}\zeta \left(3\right)+\frac{\pi ^3}{24}\ln \left(2\right)+\frac{\pi }{6}\ln ^3\left(2\right)$$

Answer 3

This is not an answer, Cornel's solution mentioned in comment is already quite elegant. Instead I provide some remarks.

---

Generalizations:

$$\int_0^{\pi/2} x^3 \cot x \log^2(\cos x) \,dx = -3 \pi \operatorname{Li}_5\left(\frac{1}{2}\right)-3 \pi \operatorname{Li}_4\left(\frac{1}{2}\right) \log (2)-\frac{3 \pi^3 \zeta (3)}{32}+\frac{141 \pi \zeta (5)}{64}-\frac{9}{16} \pi \zeta (3) \log^2(2)-\frac{1}{10} \pi \log^5(2)+\frac{1}{8} \pi^3 \log^3(2)+\frac{11}{480} \pi^5 \log (2) $$

$$\int_0^{\pi/2} x \cot x \log^4(\cos x) \, dx = -6 \pi \operatorname{Li}_5\left(\frac{1}{2}\right)-6 \pi \operatorname{Li}_4\left(\frac{1}{2}\right) \log (2)-\frac{3 \pi ^3 \zeta (3)}{32}+\frac{237 \pi \zeta (5)}{64}-\frac{9}{8} \pi \zeta (3) \log^2(2)-\frac{1}{10} \pi \log^5(2)+\frac{1}{4} \pi ^3 \log^3(2)+\frac{19}{480} \pi^5 \log (2)$$ similar evaluations also exist for $\int_0^{\pi/2} x^a \cot x \log^b(\cos x) \log^c(\sin x) \, dx$ with $a$ odd, $b,c$ positive integers with $a+b+c = 5$.

In OP's question, as well as two examples above, we observe that the results are all "divisible by $\pi$" (each term is multiplied by $\pi$). More generally, when $a$ is odd, $$\int_0^{\pi/2} x^a \cot x \log^b(\cos x) \log^c(\sin x) \, dx = \pi \times (\text{Some alternating Euler sums of weight }a+b+c)$$ When $a$ is even, then $\pi$-factor no longer appears, for example $$\int_0^{\pi /2} x^2 \cot x\ln (\cos x) \, \mathrm{d}x = - \frac{\pi^4}{720} + \frac{\ln^42}{24} - \frac{\pi^2\ln^22}{6} + \operatorname{Li}_4\left(\frac{1}{2}\right)$$

Answer 4

$\color{green}{\textbf{Version of 15.05.21.}}$

$\color{brown}{\textbf{Primary transformations.}}$

Substitution in the form of $$x=\arctan y,\quad \cos^2 x=\dfrac1{1+y^2},\quad \cot x = \dfrac1y,\quad \text dx = \dfrac{\text dy}{1+y^2}\tag1$$ presents the given integral in the form of $$I=\int\limits_0^{\large\frac\pi2} x \cot x\ln^2(\cos x)\,\text dx =\dfrac14\int\limits_0^\infty \arctan y \ln^2\left(1+y^2\right)\,\dfrac{\text dy}{y(1+y^2)}\tag2.$$ This allows partitionally use my answer to the similar question.

Is known the integral $$\int\limits_0^\infty\dfrac{\ln x\,\text dx}{(x+a)(x+b)} =\dfrac{\ln^2a-\ln^2b}{2a-2b},\quad(\Re a>0,\;\Re b>0).\tag3$$

Then $$\dfrac1y\arctan y\ln(1+y^2) = \dfrac i{2y}(\ln(1-iy)-\ln(1+iy))(\ln(1-iy)+\ln(1+iy))$$ $$ = 2\,\dfrac{\ln^2(1-iy)-\ln^2(1+iy)}{2(1-iy)-2(1+iy)} = 2\int\limits_0^\infty\dfrac{\ln z\,\text dz}{(z+1-iy)(z+1+iy)},$$ $$\dfrac1y\arctan y\ln(1+y^2)= 2\int\limits_0^\infty\dfrac{\ln z\,\text dz}{(z+1)^2+y^2}.\tag4$$ Besides, for $\;p>0\;$ $$\int\limits_0^\infty \dfrac{\ln(1+y^2)\,\text dy}{p^2+y^2} =\pi\,\dfrac{\ln(p+1)}{p}.\tag5$$

Taking in account $(2)-(5),$ one can get $$I = \dfrac12\int\limits_0^\infty\int\limits_0^\infty \dfrac{\ln z}{(z+1)^2+y^2} \dfrac{\ln(1+y^2)}{1+y^2}\,\text dz\,\text dy$$ $$= \dfrac12\int\limits_0^\infty\int\limits_0^\infty \left(\dfrac1{1+y^2}-\dfrac1{(z+1)^2+y^2} \right)\ln(1+y^2)\,\dfrac{\ln z}{z^2+2z}\,\text dy\,\text dz,$$ $$I= \dfrac\pi2\int\limits_0^\infty \left(\ln 2-\dfrac{\ln(z+2)}{z+1}\right)\,\dfrac{\ln z}{z^2+2z}\,\text dz.\tag6$$

Considered transformations allowed to simplify the given integral. However, the obtained integral looks non-trivial too.

$\color{brown}{\textbf{Splitting.}}$

Integral $(6)$ can be splitted to the six integrals. Really, taking in account $(3),$

\begin{align} &\dfrac4\pi\,I= 2\int\limits_0^\infty \dfrac{(z\ln 2-\ln(1+\frac12z))\ln z}{z(1+z)(2+z)}\,\text dz\\[4pt] &= 2\ln2\int\limits_0^\infty \dfrac{\ln z}{(1+z)(2+z)}\,\text dz -\int\limits_0^\infty \dfrac{\ln(2z) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz\\[4pt] &= \ln^3 2 -\int\limits_0^\infty \dfrac{\ln(2) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz -\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{z(1+z)}\,\text dz +2\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{(1+z)(1+2z)}\,\text dz\\[4pt] &= \ln^3 2 -\int\limits_0^\infty \dfrac{\ln(2) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz -\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{z(1+z)}\,\text dz\\[4pt] &+\int\limits_0^\infty \dfrac{\ln^2(1+z)}{(1+z)(1+2z)}\,\text dz +\int\limits_0^\infty \dfrac{\ln^2(z)}{(1+z)(1+2z)}\,\text dz -\int\limits_0^\infty \dfrac{(\ln(z+1)-\ln z)^2}{(1+z)(1+2z)}\,\text dz. \end{align}

$\color{brown}{\textbf{Closed forms of the integrals.}}$

Four first interals of the five can be calculated by Wolfram Alpha immediately, \begin{align} &I_1 = -\int\limits_0^\infty \dfrac{\ln(2) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz = -\ln^2 2,\\[4pt] &I_2 = -\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{z(1+z)}\,\text dz = -\zeta(3),\\[4pt] &I_3 = \int\limits_0^\infty \dfrac{\ln^2(1+z)}{(1+z)(1+2z)}\,\text dz = \dfrac1{12}(21\zeta(3)+4\ln^3 2 -\pi^2 \ln4),\\[4pt] &I_4 = \int\limits_0^\infty \dfrac{\ln^2(z)}{(1+z)(1+2z)}\,\text dz = \dfrac13\,\ln2(\pi^2+\ln^2 2). \end{align}

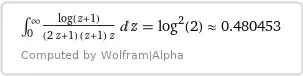
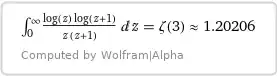
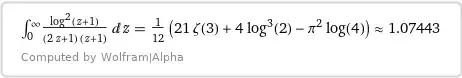
Besides, $$I_5 = -\int\limits_0^\infty \dfrac{(\ln(z+1)-\ln z)^2}{(1+z)(1+2z)}\,\text dz = -\int\limits_0^\infty \dfrac{\ln^2\left(\dfrac1z+1\right)}{z^2\left(1+\dfrac1z\right)\left(2+\dfrac1z\right)}\,\text dz,$$ $$I_5 = -\int\limits_0^\infty \dfrac{\ln^2(z+1)}{(1+z)(2+z)}\,\text dz = -\frac32\,\zeta(3).$$

Therefore, $$\dfrac4\pi I = \ln^3 2 - \ln^3 2 - \zeta(3) + \dfrac1{12}(21\zeta(3)+4\ln^3 2 -\pi^2 \ln4) + \dfrac13\,\ln2(\pi^2+\ln^2 2) -\dfrac32\,\zeta(3),$$ $$\color{green}{\mathbf{I = \dfrac\pi{6}\,\ln^3 2 - \dfrac{3\pi}{16}\,\zeta(3) + \dfrac{\pi^3}{24}\ln2.}}\tag7$$

Answer 5

A quite elegant solution.

The fact $$ \Im\left[\log^3\left(\frac{1+e^{2ix}}2\right)\right]=3x\log^2\cos x-x^3 $$

yields $$ \int_0^{\pi/2}x\cot x\log^2\cos x~d x=\frac16\Im\left[\int_{-\pi/2}^{\pi/2}\cot x\log^3\left(\frac{1+\text e^{2ix}}2\right)d x\right]+\frac13\int_0^{\pi/2}x^3\cot x~d x $$ The rest two integrals are easy. $$ \begin{align} &\int_{-\pi/2}^{\pi/2}\cot x\log^3\left(\frac{1+\text e^{2ix}}2\right)~d x \\=&\oint\frac{z+1}{z-1}\log^3\left(\frac{1+z}2\right)~\frac{d z}{2iz}\quad z=e^{2ix} \\=&2\pi~\text{Res}\left[\frac{z+1}{z-1}\log^3\left(\frac{1+z}2\right)~\frac{1}{2iz},0\right] \\=&i\pi\log^32 \end{align} $$

The contour is the unit circle with small perturbations near $z=\pm1$ . $$ \begin{align} &\int_0^{\pi/2}x^3\cot x~d x \\=&x^3\log(2\sin x)\Big|_0^{\pi/2}-3\int_0^{\pi/2}x^2\log(2\sin x)d x \\=&\frac{\pi^3}8\log2+3\int_0^{\pi/2}\sum_{n\ge1}\frac{\cos(2nx)}nx^2~d x \\=&\frac{\pi^3}8\log2+3\sum_{n\ge1}\frac{\pi(-1)^n}{4n^3} \\=&\frac{\pi^3}8\log2-\frac{9\pi}{16}\zeta (3) \end{align} $$

Where Fourier series of $\log(2\sin x)$ is applied.

Combine them and the result follows. $$ \int_0^{\pi/2}x\cot x\log^2\cos x~d x=\frac{\pi^3}{24}\log2-\frac{3\pi}{16}\zeta (3)+\frac\pi6\log^32 $$

Answer 6

Below is a real-space evaluation of the integral. Utilize \begin{align} &\int_0^1 \frac{\ln\frac{1-t}t}{1+y^2 t^2} \, \overset{s=\frac{1-t}t }{dt } =\int_0^\infty \frac{\ln s}{(s+1)^2+y^2}\overset{s\to \frac{1+y^2}s}{ds}\\ &\hspace{5mm} =\frac12 \int_0^\infty \frac{\ln(1+y^2)}{(s+1)^2+y^2}\ ds = \frac1{2y}\tan^{-1}y\ \ln(1+y^2) \end{align} to integrate as follows \begin{align} &\hspace{5mm}\int_0^{\frac\pi2} x \cot x\ln^2(\cos x) \overset{y=\tan x} {dx}\\ & =\dfrac14\int_0^\infty\,\dfrac{ \tan^{-1} y \ \ln^2\left(1+y^2\right)}{y(1+y^2)}dy\\ &= \frac12 \int_0^\infty \frac{\ln(1+y^2)}{1+y^2}\int_0^1\frac{\ln\frac{1-t}t}{1+y^2t^2}dt \ dy\\ &= \frac12 \int_0^1\int_0^\infty \frac{\ln\frac{1-t}t }{1-t^2}\left(\frac{\ln(1+y^2)}{1+y^2}-\frac{t^2 \ln(1+y^2)}{1+y^2t^2}\right)dy \ dt\\ &= \frac\pi2 \int_0^1 \frac{\ln\frac{1-t}t}{1-t^2} \left(\ln2 -t \ln\frac{1+t}t \right)dt \\ &= \frac\pi2 \int_0^1 \frac{\ln2\ln\frac{1-t}t-t \ln(1-t)\ln(1+t)}{1-t^2} \overset {t\to \frac{1-t}{1+t}}{dt}\\ &\hspace{10mm}+\frac\pi2\int_0^1 \frac{t\ln t\ln(1-t^2)}{1-t^2} \overset{1-t^2\to t^2}{dt}-\frac\pi2\int_0^1 \frac{t\ln^2t}{1-t^2} \ \overset{ibp}{dt}\\ &= \frac\pi4 \int_0^1 \frac{2\ln^2\frac{1+t}2}{1+t}-\frac{\ln2\ln(1-t)}{t} +\frac{\ln t\ln(1-t)}{t}\ dt\\ &\hspace{10mm}+\frac\pi2\int_0^1 \frac{\ln t\ln(1-t^2)}{t} {dt}-\frac\pi2 \int_0^1 \frac{\ln t\ln(1-t^2)}{t}{dt}\\ &=\frac\pi4 \left[\frac23 \ln^32-\ln2\left(-\frac{\pi^2}{6}\right)-\frac34\zeta(3)\right]+0\\ &= \frac{\pi }{6}\ln ^32+ \frac{\pi ^3}{24}\ln 2-\frac{3\pi }{16}\zeta (3) \end{align}

Answer 7

I will be using the “make everything into a sum and then integrate” method. This means that we will call it I and manipulate the integral until it can be integrable with a gamma function: $$I=\int_0^{π/2} x\cot(x)\ln^2\cos(x)\,dx=\int_0^{π/2}x\bigg(\sum_{n=0}^∞ \bigg[c_n=\frac{(-1)^n2^{2n}B_{2n}}{(2n)!}\bigg] x^{2n-1}\bigg)\bigg(-\sum_{k=1}^∞ \frac{(-1)^k\cos^k(x)}{k}\bigg)\bigg(-\sum_{m=1}^∞\frac{(-1)^m\cos^m(x)}{m}\bigg)\,dx$$ where $B_y$ are the Bernoulli Numbers.

Because all of the indices are constant from each other, they can be treated as such and moved around without needing any cauchy products are needed, using the complex definition of the cosine function and using the binomial theorem once more gets us our simplified integral to be integrated in the next step: $$\int_0^{π/2}x\bigg(\sum_{n=0}^∞c_n=x^{2n-1}\bigg)\bigg(-\sum_{k=1}^∞ \frac{(-1)^k \cos^k(x)}{k}\bigg)\bigg(-\sum_{m=1}^∞\frac{(-1)^m\cos^m(x)}{m}\bigg)\,dx = \sum_{n=0}^∞ c_n\sum_{k=1}^∞ \sum_{m=1}^∞ \frac{(-1)^{m+k}}{mk} \int_0^{π/2}x^{2n} \frac{(e^{\mathit ix}+ e^{-\mathit ix})^{m+k}}{2^{m+k}} \, dx = \sum_{n=0}^∞ c_n\sum_{k=1}^∞ \sum_{m=1}^∞ \frac{(-1)^{m+k}}{mk} \int_0^{π/2}x^{2n}2^{-(m+k)}\sum_{j=0}^{m+k} \binom{m+k}{j}e^{-ijx} \, dx= \sum_{n=0}^∞ c_n\sum_{k=1}^∞ \sum_{m=1}^ ∞\frac{(-1)^{m+k}}{2^{m+k}mk}\sum_{j=0}^{m+k} \binom{m+k}{j} \int_0^{π/2} x^{2n} e^{-ijx}dx$$

By the way, here is proof this equals @pisco’s answer. From here on out, desmos cannot handle complex numbers. This means that if the following steps are correct, them we have a summation form of I because there are no restrictions on the binomial theorem that would give us conflicts and because this method is similar to the generalized Sophomore’s Dream integral with a sum and then a general powers of $x\ln(x)$ integration where here there is a general power of $x\cos(x)$ except with two more complicated powers.

Finally, we can integrate by using the generalized incomplete gamma function as the integral looks like the main definition of the gamma function and put it into a few forms including the summation form of the gamma function. As I am not completely as versed in substitution for finding the integral in terms of this function, a bit of machine help was used:

$$\sum_{n=0}^∞ c_n\sum_{k=1}^∞ \sum_{m=1}^∞ \frac{(-1)^{m+k}}{2^{m+k}mk} \sum_{j=0}^{m+k} \binom{m+k}{j} \int_0^{π/2} x^{2n} e^{-ijx}\,dx= \sum_{n=0}^∞ c_n\sum_{k=1}^∞ \sum_{m=1}^∞ \frac{(-1)^{m+k}}{2^{m+k}mk}\sum_{j=0}^{m+k} \binom{m+k}{j}(j^{-1}\mathit i・\mathit i^{-2n}j^{-2n}Γ(2n+1,ijx)|_0^{π/2})= \sum_{n=0}^∞ \frac{(-1)^n2^{2n}B_{2n}}{(2n)!}\sum_{k=1}^ ∞\sum_{m=1}^∞ \frac{(-1)^{m+k}}{2^{m+k}mk}\sum_{j=0}^{m+k} \binom{m+k}{j}\frac{(-1)^n\mathit iΓ(2n+1,\frac{π\mathit ij}{2},0)}{j^{2n+1}}= \sum_{n=0}^∞ \frac{B_{2n}}{(2n)!} \sum_{k=1}^ ∞\sum_{m=1}^∞ \frac{(-1)^{m+k}}{2^{k+m-2n}mk}\sum_{j=0}^{m+k} \binom{m+k}{j}\frac{\mathit iΓ(2n+1,\frac{π\mathit ij}{2},0)}{j^{2n+1}}= \sum_{n=0}^∞ \frac{2^{2n}B_{2n}}{(2n)!}\sum_{k=1}^∞ \sum_{m=1}^∞ \frac{1}{(-2)^{m+k}mk} \sum_{j=0}^{m+k} \binom{m+k}{j}\frac{\mathit i(Γ(2n+1,\frac{π\mathit ij}{2})-(2n))!}{j^{2n+1}}= \sum_{n=1}^ ∞\frac{B_{2(n-1)}}{(2(n-1))!}\sum_{k=1}^∞ \sum_{m=1}^∞ \frac{(-1)^{m+k}}{mk}\sum_{j=0}^{m+k} \binom{m+k}{j}\frac{(-\mathit i)^{j-1}}{j^{2n-1}}\sum_{p=0}^{2(n-1)} \frac{(π\mathit i)^p}{2^{k+m+2(1-n)+p}p!}$$

I will try to evaluate this expression if I can. I apologize for the unwanted solution, but this took some effort to put together.:

$$I=\sum_{n=0}^∞ \sum_{k=1}^∞ \sum_{m=1}^∞ \sum_{j=0}^{m+k} \binom{m+k}{j} \frac{(-1)^{m+k} B_{2n} \mathit iΓ(2n+1,\frac{π\mathit ij}{2},0)}{2^{k+m-2n} j^{2n+1} mk (2n)!}=\sum_{n=0}^∞ \sum_{k=1}^∞ \sum_{m=1}^∞ \sum_{j=0}^{m+k} \binom{m+k}{j}\frac{(-1)^nc_n \mathit iΓ(2n+1,\frac{π\mathit ij}{2})-(2n)!}{(-2)^{k+m} j^{2n+1} mk}= \sum_{n=0}^∞ \sum_{k=1}^∞ \sum_{m=1}^∞ \sum_{j=0}^{m+k} \binom{m+k}{j}\frac{(-1)^nc_n \mathit iΓ(2n+1,\frac{π\mathit ij}{2})}{(-2)^{k+m} j^{2n+1} mk}-\sum_{n=0}^∞ \sum_{k=1}^∞ \sum_{m=1}^∞ \sum_{j=0}^{m+k} \binom{m+k}{j}\frac{2^{2n} B_{2n}\mathit i}{(-2)^{k+m} j^{2n+1} mk} $$

Let there be a focus on the second term: $$S_1-I=S_2= \sum_{n=0}^∞ \sum_{k=1}^∞ \sum_{m=1}^∞ \sum_{j=0}^{m+k} \binom{m+k}{j} \frac{2^{2n} B_{2n}\mathit i}{(-2)^{k+m} j^{2n+1} mk} = \mathit i\sum_{n=0}^∞ 2^{2n} B_{2n} \sum_{k=1}^∞ \frac{(-1)^{k}}{2^kk} \sum_{m=1}^∞ \frac{(-1)^{m}}{2^mm} \sum_{j=0}^{m+k} \binom{m+k}{j} j^{-(2n+1)}$$

I will fix this soon enough ...

As always, there is not much of a way to check the post integration answer, so please point out any errors here and give me feedback. As a side note, the index switch was needed to expand out the generalized incomplete gamma function with the 0 in the argument and exponential for this expansion for n>0 was already simplified.