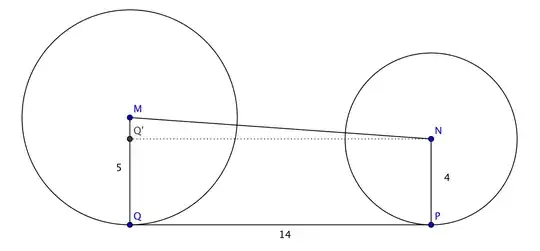
I have the following problem:
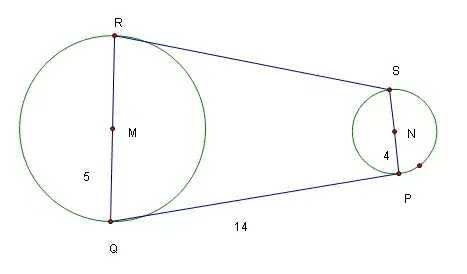
In my class, we did a majorly complicated method to figure this out but I think there is a better way to do this... Here is the exact problem:
A belt fits snugly around the two circular pulleys shown.
Find the distance between the centers of the pulleys. Round to the nearest hundredth.
The method we used required that I create this huge triangle across the page. It didn't sound like the best way to do it. Does anybody have a "none-hacked" way to do it (as in, a more straight forward procedure)?
EDIT
I'm sorry about this, yes, the diagram is misleading, I had to recreate the image in an annoying program. Yes, lines RS and line QP are both tangent to both circles. Sorry about that, I never explained the context of the question.